ta có AB =12cm là 1 cạnh của tam cân ABC;Tương tự với cạnh BC =6cm và là 1 cạnh của tam giác cân ABC

mà AB không bằng BC nên chỉ có 2 trường hợp trong tam giác cân là AB = AC và BC =CA

suy ra cạnh AC còn lại sẽ có 2 giá trị là 12cm và 6cm

Câu hỏi của trần thị nhài - Toán lớp 7 - Học toán với OnlineMath

a, Diện tích tam giác ABC là 

\(\dfrac{1}{2}.12.15=90cm^2\)

b, thiếu đề rồi bạn 

a. Tổng BC và CA là:

12 + 7= 19(cm)

b. Chu vi tam giác ABC là:

12 + 19= 31(cm)

Đ/s: a: 19cm

       b:31cm

=100x5

Ta có: Δ ABC ∼ Δ A'B'C'

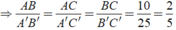
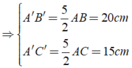
Chọn đáp án D.

Ta có: Δ ABC đồng dạng Δ A'B'C'

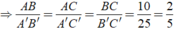
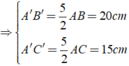
Chọn đáp án D.

Lời giải:

Gọi $H$ là chân đường cao kẻ từ $A$. Vì $ABC$ cân tại $A$ nên $H$ là trung điểm $BC$

Ta có:

\(S_{ABC}=\frac{AH.BC}{2}=\frac{h_C.AB}{2}\)

\(\Rightarrow BC=\frac{h_C.AB}{AH}=\frac{12AB}{15,6}=\frac{10}{13}AB\)

\(\Rightarrow BH=\frac{5}{13}AB\)

Áp dụng định lý Pitago:

$AH^2=AB^2-BH^2=AB^2-(\frac{5}{13}AB)^2$

$\Leftrightarrow 15,6^2=\frac{144}{169}AB^2$

$\Rightarrow AB=16,9$

$\Rightarrow BC=\frac{10}{13}AB=13$ (cm)

Hình vẽ:

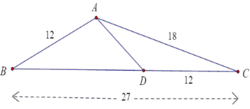
Ta có

A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A

Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)

Nên ΔACB ~ ΔDCA (c.g.c)

⇒ A C D C = A B D A ⇔ 3 2 = 12 D A ⇒ D A   = 2.12 3 =   8 c m

Đáp án: D