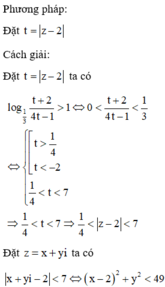tìm các số tự nhiên x,y,z thỏa mãn đẳng thức 26x 25y 24z
NM
Những câu hỏi liên quan
Tìm các số tự nhiên x,y,z thỏa mãn đẳng thức 2006^x=2005^y+2004^z
Ta có: \(2006^x=2005^y+2004^z>1\)
\(\Rightarrow x\ge1\)
Vì \(2006^x\) là số chẵn, \(2005^y\) là số lẻ
nên \(2004^z\) là số lẻ
\(\Rightarrow z=0\)
Lúc đó, ta có phương trình: \(2006^x=2005^y+1\)
Lại có: \(\hept{\begin{cases}2005\equiv1\left(mod4\right)\Rightarrow2005^y+1\equiv2\left(mod4\right)♣\\2006=4m+2\Rightarrow2006^x=4k+2^x\end{cases}}\)
Với \(x\ge2\) thì \(2006^x\) chia hết cho 4, mâu thuẫn với ♣.
Vậy \(x=y=1;z=0\)
Đúng 0
Bình luận (0)
+ Với x = 0 thì 2006x = 20060 = 1, vô lí vì 2005y + 2004z > hoặc = 2
=> x > 0
=> 2006x là số chẵn mà 2005y luôn lẻ với mọi y là số tự nhiên
=> 2004z là số lẻ => z = 0
Ta có: 2006x = 2005y + 20040 = 2005y + 1
+ Ta thấy với x = 1; y = 1 thỏa mãn đề bài: 2006 = 2005 + 1, chọn
+ Với x, y > 1
Do 2005 chia 4 dư 1, mũ lên bao nhiêu vẫn chia 4 dư 1 => 2005y chia 4 dư 1
Mà 1 chia 4 dư 1 => 2005y + 1 chia 4 dư 2, vô lí vì 2006x với x > 1 chia hết cho 4
Vậy x = 1; y = 1; z = 0
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các số tự nhiên x; y; z thỏa mãn đẳng thức: 2006x=2005y+2004z
Có 1 trường hợp là : x = 1 ; y = 1 ; z = 0
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm các số tự nhiên x,y,z thỏa mãn đẳng thức 26x=25y+24z
Gọi M(x;y) là các điểm biểu diễn cho số phức z thỏa mãn
log
1
3
z
−
2
+
2
4
z
−
2
−
1
1.
Khi đó
x
;
y...
Đọc tiếp
Gọi M(x;y) là các điểm biểu diễn cho số phức z thỏa mãn log 1 3 z − 2 + 2 4 z − 2 − 1 > 1. Khi đó x ; y thỏa mãn hệ thức nào dưới đây?
A. x + 2 2 + y 2 > 49
B. x + 2 2 + y 2 < 49
C. x − 2 2 + y 2 < 49
D. x − 2 2 + y 2 > 49
Tìm các số nguyên tố x,y,z thỏa mãn đẳng thức :x^y+1=z
Ta thấy nếu x lẻ => VT chẵn => z chẵn ko phải số nguyên tố
Vậy x chỉ là số chẵn mà nguyên tố => x= 2
Với y=2 => z= 5 thỏa đk đề bài
Nếu y>2 => y lẻ (vì y nguyên tố)
=> y =2k +1
=> 2^(2k+1) +1 = 2.4^k + 1 = 2.(3p+1) + 1 = 3m
Như vậy khi x=2 và y nguyên tố > 2 thì VT luôn chia hết cho 3
=>z chia hết cho 3 không thỏa đk
Vậy x=y=2; z= 5 là duy nhất
Đúng 0
Bình luận (0)
bạn ơi ! Bạn please cho mình cách giải v~
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Tìm các số tự nhiên x, y, z nhỏ nhất khác 0 thoả mãn: 20x = 25y = 30z
2. Tìm tất cả các số nguyên n biết: (2n + 1)\(⋮\)(n-1).
Bài 1:
Đặt $20x=25y=30z=t$ với $t$ là số tự nhiên khác 0.
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{25}; z=\frac{t}{30}$
Để $x,y,z$ là stn thì $t\vdots 20,25,30$
$\Rightarrow t=BC(20,25,30)$
Để $x,y,z$ nhỏ nhất và khác 0 thì $t$ nhỏ nhất và khác 0
$\Rightarrow t=BCNN(20,25,30)$ sao cho $t\neq 0$
$\Rightarrow t=300$
$\Rightarrow x=\frac{t}{20}=\frac{300}{20}=15, y=\frac{t}{25}=\frac{300}{25}=12; z=\frac{300}{30}=10$
Đúng 1
Bình luận (0)
Bài 2:
$2n+1\vdots n-1$
$\Rightarrow 2(n-1)+3\vdots n-1$
$\Rightarrow 3\vdots n-1$
$\Rightarrow n-1\in \left\{1; -1; 3;-3\right\}$
$\Rightarrow n\in \left\{3; 0; 4; -2\right\}$
Đúng 2
Bình luận (0)
Tìm các số tự nhiên x,y,z thỏa mãn : x+y+z= xyz
Xem thêm câu trả lời
Cho x;y;z>0 ;x+y+z=1
tìm giá trị nhỏ nhất của biểu thức
P=\(\frac{15x^2}{z}+\frac{5y^2}{36x}+\frac{24z^2}{25y}\)
a) Chứng minh đa thức x2 + x + 1 không có nghiệm.
b) Cho các số không âm x,y,z thỏa mãn 8x+3y = 29 và 9x + 1008z = 9 .Tìm giá trị lớn nhất của biểu thức A = 26x + 3y + 2015z.