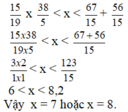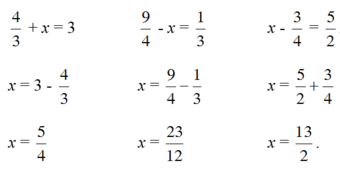Tìm x biết 4500 : x +385=394
BT
Những câu hỏi liên quan
b) Tìm số tự nhiên x biết:
15 19 x 38 5 < x < 67 15 + 56 15
tìm x,y,z biết (7x-5y)^2018+(3x-2z)^2020+(xy+yz+z -4500)^2022=0
hỏi khó thế anh zai
a) Tìm X: X - 4368 = 3484 x 4
b) Tính bằng cách thuận tiện nhất 49 x 385 – 39 x 385
a)\(x-4368=13936=>x=13936+4368=18304\)
b)\(385*(49-39)=>385*10=3850\) nhé
Đúng 2
Bình luận (8)
x - 4368 = 3484 x 4
x - 4368 = 13936
x = 13936 + 4368
x = 18304
b) 49 x 385 - 39 x 385
= 385 x ( 49 - 39 )
= 385 x 10
= 3850
Đúng 2
Bình luận (0)
x - 4368 = 3484 x 4
x - 4368 = 13936
x = 13936 + 4368
x = 18304
b) 49 x 385 - 39 x 385
= 385 x ( 49 - 39 )
= 385 x 10
= 3850
Đúng 1
Bình luận (0)
Tìm x biết 7/4*(3333/1212+3333/2020+3333/3030+3333/4242+3333/5656)*x=-385/32
a. Thực hiện phép tính:
3,54 x 73 + 0,23 x 25 + 3,54 x 27 + 0,17 x 25
b. Tìm số tự nhiên x biết:
15 19 x 38 5 < X < 67 15 + 56 15
a. 3,54 x 73 + 0,23 x 25 + 3,54 x 27 + 0,17 x 25
= ( 3,54 x 73 + 3,54 x 27) + (0,23 x 25 + 0,17 x 25)
= 3,54 x (73 + 27) + 25 x (0,23 + 0,17)
= 3,54 x 100 + 25 x 0,4
= 354 + 10
= 364
b. 15 19 x 38 5 < X < 67 15 + 56 15
15 × 38 19 × 5 < x < 67 + 56 15
3 × 2 1 × 1 < x < 123 15
6 < x < 8,2
Vậy x = 7 hoặc x = 8.
Đúng 0
Bình luận (0)
Tìm x:
4 3 + x = 3 9 4 - x = 1 3 x - 3 4 = 5 2
tìm x
x2+5x+4500=0
\(x^2+5x+4500=0\)
\(\Delta=b^2-4ac=5^2-4.1.4500=25-18000=-17975\)
Vì \(\Delta=-17975< 0\)nên phương trình vô nghiệm
Hok tốt
tìm x
x2 +5x-4500=0
\(\Delta=\left(-5\right)^2-4.1.\left(-4500\right)=25+18000=18025>0\)
\(\Rightarrow\)Phương trình có 2 nghiệm phân biệt là:
\(x_1=\frac{-5-\sqrt{18025}}{2}=\frac{-5-5\sqrt{721}}{2}\)và \(x_2=\frac{-5+\sqrt{18025}}{2}=\frac{-5+5\sqrt{721}}{2}\)
Vậy \(x=\frac{-5\pm5\sqrt{721}}{2}\)
1.
The first term is, x2 its coefficient is 1 .
The middle term is, +5x its coefficient is 5 .
The last term, "the constant", is -4500
Step-1 : Multiply the coefficient of the first term by the constant 1 • -4500 = -4500
Step-2 : Find two factors of -4500 whose sum equals the coefficient of the middle term, which is 5 .
| -4500 | + | 1 | = | -4499 | ||
| -2250 | + | 2 | = | -2248 | ||
| -1500 | + | 3 | = | -1497 | ||
| -1125 | + | 4 | = | -1121 | ||
| -900 | + | 5 | = | -895 | ||
| -750 | + | 6 | = | -744 |
For tidiness, printing of 30 lines which failed to find two such factors, was suppressed
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
2.2.1 Find the Vertex of y = x2+5x-4500
Parabolas have a highest or a lowest point called the Vertex . Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) . We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero).
Each parabola has a veral line of symmetry that passes through its vertex. Because of this symmetry, the line of symmetry would, for example, pass through the midpoint of the two x -intercepts (roots or solutions) of the parabola. That is, if the parabola has indeed two real solutions.
Parabolas can model many real life situations, such as the height above ground, of an object thrown upward, after some period of time. The vertex of the parabola can provide us with information, such as the maximum height that object, thrown upwards, can reach. For this reason we want to be able to find the coordinates of the vertex.
For any parabola,Ax2+Bx+C,the x -coordinate of the vertex is given by -B/(2A) . In our case the x coordinate is -2.5000
Plugging into the parabola formula -2.5000 for x we can calculate the y -coordinate :
y = 1.0 * -2.50 * -2.50 + 5.0 * -2.50 - 4500.0
or y = -4506.250
3.
Root plot for : y = x2+5x-4500
Axis of Symmetry (dashed) {x}={-2.50}
Vertex at {x,y} = {-2.50,-4506.25}
x -Intercepts (Roots) :
Root 1 at {x,y} = {-69.63, 0.00}
Root 2 at {x,y} = {64.63, 0.00}
Solve Quadra Equation by Completing The Square
2.2 Solving x2+5x-4500 = 0 by Completing The Square .
Add 4500 to both side of the equation :
x2+5x = 4500
Now the clever bit: Take the coefficient of x , which is 5 , divide by two, giving 5/2 , and finally square it giving 25/4
Add 25/4 to both sides of the equation :
On the right hand side we have :
4500 + 25/4 or, (4500/1)+(25/4)
The common denominator of the two fractions is 4 Adding (18000/4)+(25/4) gives 18025/4
So adding to both sides we finally get :
x2+5x+(25/4) = 18025/4
Adding 25/4 has completed the left hand side into a perfect square :
x2+5x+(25/4) =
(x+(5/2)) • (x+(5/2)) =
(x+(5/2))2
Things which are equal to the same thing are also equal to one another. Since
x2+5x+(25/4) = 18025/4 and
x2+5x+(25/4) = (x+(5/2))2
then, according to the law of transitivity,
(x+(5/2))2 = 18025/4
We'll refer to this Equation as Eq. #2.2.1
The Square Root Principle says that When two things are equal, their square roots are equal.
Note that the square root of
(x+(5/2))2 is
(x+(5/2))2/2 =
(x+(5/2))1 =
x+(5/2)
Now, applying the Square Root Principle to Eq. #2.2.1 we get:
x+(5/2) = √ 18025/4
Subtract 5/2 from both sides to obtain:
x = -5/2 + √ 18025/4
Since a square root has two values, one positive and the other negative
x2 + 5x - 4500 = 0
has two solutions:
x = -5/2 + √ 18025/4
or
x = -5/2 - √ 18025/4
Note that √ 18025/4 can be written as
√ 18025 / √ 4 which is √ 18025 / 2
4. 2.3 Solving x2+5x-4500 = 0 by the Quadra Formula .
According to the Quadra Formula, x , the solution for Ax2+Bx+C = 0 , where A, B and C are numbers, often called coefficients, is given by :
- B ± √ B2-4AC
x = ————————
2A
In our case, A = 1
B = 5
C = -4500
Accordingly, B2 - 4AC =
25 - (-18000) =
18025
Applying the quadra formula :
-5 ± √ 18025
x = ———————
2
Can √ 18025 be simplified ?
Yes! The prime factorization of 18025 is
5•5•7•103
To be able to remove something from under the radical, there have to be 2 instances of it (because we are taking a square i.e. second root).
√ 18025 = √ 5•5•7•103 =
± 5 • √ 721
√ 721 , rounded to 4 decimal digits, is 26.8514
So now we are looking at:
x = ( -5 ± 5 • 26.851 ) / 2
Two real solutions:
x =(-5+√18025)/2=(-5+5√ 721 )/2= 64.629
or:
x =(-5-√18025)/2=(-5-5√ 721 )/2= -69.629
1.Tính nhanh
a]385 x 385 +385 x 615
2.tìm X
a]6 x [X +7545] =28542 x 6 b][X :4] x 8 = 9 x 8
1. 385 x 385+ 385 x 615 = 385 ( 385 + 615)
= 385 x 1000
= 385000
2a) 6 x (X + 7545) = 28542 x6
6X + 45270 = 171252
6X = 125982
x= 125982:6
x= 20997
b) (X : 4) x8 = 9 x 8
( X :4 ) x 8 = 72
X : 4 = 72 :8
X : 4 = 9
x = 9 x 4
X= 36\(\)