Hình bao bởi mặt đáy là một đa giác đều và các mặt bên là các tam giác
bằng nhau có chung đỉnh là:
A. Hình hộp chữ nhật C. Hình nón
B. Hình chóp đều D. Hình lăng trụ đều
Xem thêm câu trả lời
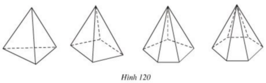
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
Chóp tam giác đều
Chóp tứ giác đều
Chóp ngũ giác đều
Chóp lục giác đều
Đáy
Tam giác đều
Mặt bên
Tam giác cân
Số cạnh đáy
5
Số cạnh
10
Số mặt
5
Đọc tiếp
Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | |||
| Mặt bên | Tam giác cân | |||
| Số cạnh đáy | 5 | |||
| Số cạnh | 10 | |||
| Số mặt | 5 |
| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |
Đúng 0
Bình luận (0)
Lăng trụ đều được tạo bởi : A.hai đáy là hai hình tam giác đều bằng nhau mặt bên là các hình chữ nhật B. hai đáy là 2 đa giác mặt bên là các hình chữ nhật C. hai đáy là hai tam giác đều bằng nhau và các mặt bên là các hình chữ nhật bằng nhau D. đáp án khác
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp SABC A.
V
a
3
B.
V
a
3
2
C.
V
3
a
3
2
D.
V...
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp SABC
A. V = a 3
B. V = a 3 2
C. V = 3 a 3 2
D. V = 3 a 3
Đáp án A
Gọi H là trung điểm AB. Ta có 2 tam giác SAB và ABC đều và bằng nhau nên SH = CH= a 3 . Mà S Δ A B C = a 2 3 ⇒ V S . A B C = 1 3 a 2 3 . a 3 = a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC A.
V
a
3
B.
V
a
3
2
C.
V
3
a
3
2
D.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC
A. V = a 3
B. V = a 3 2
C. V = 3 a 3 2
D. V = 3 a 3
Đáp án A
Gọi H là trung điểm AB. Ta có 2 tam giác SAB và ABC đều và bằng nhau nên SH = CH = a 3 . Mà S Δ A B C = a 2 3 ⇒ V S . A B C = 1 3 a 2 3 . a 3 = a 3
Đúng 0
Bình luận (0)
Câu 07:
Lăng trụ đều tạo bởi:
A.
Hai đáy là hai đa giác, mặt bên là các hình chữ nhật
B.
Hai đáy là hai đa giác đều bằng nhau, mặt bên là các hình chữ nhật bằng nhau
C.
Hai đáy là hai đa giác đều bằng nhau, mặt bên là các hình chữ nhật
D.
Đáp án khác
Hình chóp tam giác đều SABC có đáy là tam giác đều ABC, AB a; góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của hình chóp. A. V
a
3
12
B. V
a
3
2
24
C. V
a
3
3
16...
Đọc tiếp
Hình chóp tam giác đều SABC có đáy là tam giác đều ABC, AB = a; góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của hình chóp.
A. V = a 3 12
B. V = a 3 2 24
C. V = a 3 3 16
D. V = a 3 6 36
Cho hình chóp tam giác đều đáy có cạnh bằng a, góc tạo bởi các mặt bên và đáy bằng 60°. Thể tích khối chóp là: A.
V
a
3
3
24
B.
V
a
3
6
24
C.
V...
Đọc tiếp
Cho hình chóp tam giác đều đáy có cạnh bằng a, góc tạo bởi các mặt bên và đáy bằng 60°. Thể tích khối chóp là:
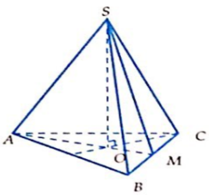
A. V = a 3 3 24
B. V = a 3 6 24
C. V = a 3 3 8
D. V = a 3 8
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là: A.
a
3
6
B.
a
3
3
C.
a
3
8
D.
2
a
3
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
A. a 3 6
B. a 3 3
C. a 3 8
D. 2 a 3
Đáp án C
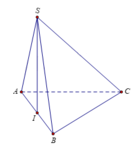
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
![]()
![]()
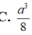
![]()