Hãy tìm giá trị ngoại lệ của mẫu số liệu: 37; 12; 3; 9; 10; 9; 12; 3; 10.
Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và các giá trị ngoại lệ của các mẫu số liệu sau:
a) 6; 8; 3; 4; 5; 6; 7; 2; 4.
b) 13; 37; 64; 12; 26; 43; 29; 23.
a)
+) Số trung bình \(\overline x = \frac{{6 + 8 + 3 + 4 + 5 + 6 + 7 + 2 + 4}}{9} = 5\)
+) phương sai hoặc \({S^2} = \frac{1}{9}\left( {{6^2} + {8^2} + ... + {4^2}} \right) - {5^2} = \frac{{10}}{3}\)
=> Độ lệch chuẩn \(S = \sqrt {\frac{{10}}{3}} \approx 1,8\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 3; 4; 4; 5; 6; 6; 7; 8.
+) Khoảng biến thiên: \(R = 8 - 2 = 6\)
Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu 2; 3; 4; 4. Do đó \({Q_1} = 3,5\)
\({Q_3}\) là trung vị của nửa số liệu: 6; 6; 7; 8. Do đó \({Q_3} = 6,5\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 6,5 - 3,5 = 3\)
+) x là giá trị ngoại lệ trong mẫu nếu \(x > 6,5 + 1,5.3 = 11\) hoặc \(x < 3,5 - 1,5.3 = - 1\)
Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.
b)
+) Số trung bình \(\overline x = \frac{{13 + 37 + 64 + 12 + 26 + 43 + 29 + 23}}{8} = 30,875\)
+) phương sai hoặc \({S^2} = \frac{1}{8}\left( {{{13}^2} + {{37}^2} + ... + {{23}^2}} \right) - 30,{875^2} \approx 255,8\)
=> Độ lệch chuẩn \(S \approx 16\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 12; 13; 23; 26; 29; 37; 43; 64.
+) Khoảng biến thiên: \(R = 64 - 12 = 52\)
Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
\({Q_2} = {M_e} = 27,5\)
\({Q_1}\) là trung vị của nửa số liệu 12; 13; 23; 26. Do đó \({Q_1} = 18\)
\({Q_3}\) là trung vị của nửa số liệu: 29; 37; 43; 64. Do đó \({Q_3} = 40\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 40 - 18 = 22\)
+) x là giá trị ngoại lệ trong mẫu nếu \(x > 40 + 1,5.22 = 73\) hoặc \(x < 18 - 1,5.22 = - 15\)
Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.
Bảng sau thống kê số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam.

(Nguồn: worldometers.info)
a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?
b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.
Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
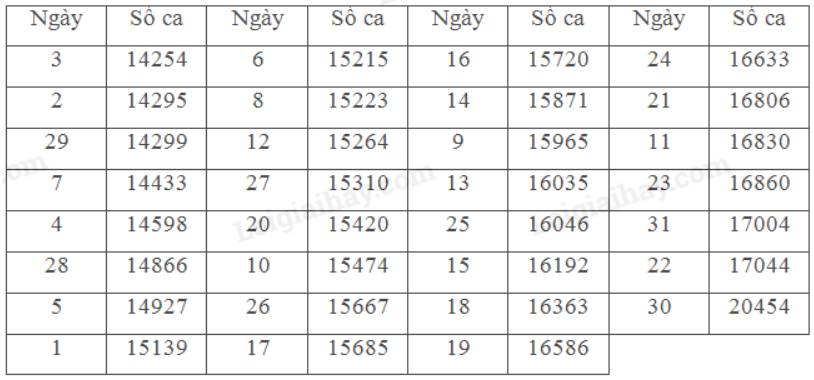
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)

c) Ta có:

• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)
Cho mẫu số liệu gồm bốn số tự nhiên khác nhau và khác 0, biết số trung bình là 6 và số trung vị là 5. Tìm các giá trị của mẫu số liệu đó sao cho hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
A. 3;4;6;11
B. 2;4;7;11
C. 3;5;6;11
D. 2;4;6;12
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có 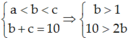 hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị của các mẫu số liệu sau:
a)
Giá trị | -2 | -1 | 0 | 1 | 2 |
Tần số | 10 | 20 | 30 | 20 | 10 |
b)
Giá trị | 0 | 1 | 2 | 3 | 4 |
Tần số | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
a)
+) Số trung bình \(\overline x = \frac{{ - 2.10 + ( - 1).10 + 0.30 + 1.20 + 2.10}}{{10 + 20 + 30 + 20 + 10}} = 0\)
+) phương sai hoặc \({S^2} = \frac{1}{90}\left( {10.{{( - 2)}^2} + 10.{{( - 1)}^2} + ... + {{10.2}^2}} \right) - {0^2} = 4 \over 3\)
=> Độ lệch chuẩn \(S \approx 1,155\)
+) Khoảng biến thiên: \(R = 2 - ( - 2) = 4\)
Tứ phân vị: \({Q_2} = 0;{Q_1} = - 1;{Q_3} = 1\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 1 - ( - 1) = 2\)
b) Giả sử cỡ mẫu \(n = 10\). Khi đó mẫu số liệu trở thành:
Giá trị | 0 | 1 | 2 | 3 | 4 |
Tần số | 1 | 2 | 4 | 2 | 1 |
+) Số trung bình \(\overline x = \frac{{0.0,1 + 1.0,2 + 2.0,4 + 3.0,2 + 4.0,1}}{{0,1 + 0,2 + 0,4 + 0,2 + 0,1}} = 2\)
+) phương sai hoặc \({S^2} = \frac{1}{1}\left( {0,{{1.0}^2} + 0,{{2.1}^2} + ... + 0,{{1.4}^2}} \right) - {2^2} = 1,2\)
=> Độ lệch chuẩn \(S \approx 1,1\)
+) Khoảng biến thiên: \(R = 4 - 0 = 4\)
Tứ phân vị: \({Q_2} = 2;{Q_1} = 1;{Q_3} = 3\)
+) Khoảng tứ phân vị: \({\Delta _Q} = 3 - 1 = 2\)
Tỉ lệ thất nghiệp ở một số quốc gia vào năm 2007 (đơn vị %) được cho như sau:
7,8 3,2 7,7 8,7 8,6 8,4 7,2 3,6
5,0 4,4 6,7 7,0 4,5 6,0 5,4
Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.
Sắp xếp theo thứ tự không giảm.:
3,2 3,6 4,4 4,5 5,0 5,4 6,0 6,7 7,0 7,2 7,7 7,8 8,4 8,6 8,7
Vì n=15 nên \({Q_2} = 6,7\)
\({Q_1} = 4,5;{Q_3} = 7,8\)
\({\Delta _Q} = {Q_3} - {Q_1} = 7,8 - 4,5 = 3,3\)
\({Q_3} + 1,5.{\Delta _Q} = 12,75\)
\({Q_1} - 1,5{\Delta _Q} = - 0,45\)
Ta thấy không có giá trị nào dưới -0,45 và trên 12,75 nên không có giá trị bất thường.
Bài 5: Cho phân số 25/37 hãy tìm số tự nhiên C sao cho khi đem mẫu số của phân số đó trừ đi C và giữ nguyên tử số ta được phân số có giá trị bằng 5/6
Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:
a)
Giá trị | 23 | 25 | 28 | 31 | 33 | 37 |
Tần số | 6 | 8 | 10 | 6 | 4 | 3 |
b)
Giá trị | 0 | 2 | 4 | 5 |
Tần số tương đối | 0,6 | 0,2 | 0,1 | 0,1 |
a) \(23;{\rm{ }}41;{\rm{ }}71;{\rm{ }}29;{\rm{ }}48;{\rm{ }}45;{\rm{ }}72;{\rm{ }}41\).
+) Số trung bình: \(\overline x = \frac{{23 + 41 + 71 + 29 + 48 + 45 + 72 + 41}}{8} = 46,25\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(23;{\rm{ }}29;{\rm{ }}41;{\rm{ }}41;\;{\rm{ }}45;{\rm{ }}48;\;71;72\)
Bước 2: \(n = 8\), là số chẵn nên \({Q_2} = {M_e} = \frac{1}{2}(41 + 45) = 43\)
\({Q_1}\) là trung vị của nửa số liệu \(23;{\rm{ }}29;{\rm{ }}41;{\rm{ }}41\). Do đó \({Q_2} = \frac{1}{2}(29 + 41) = 35\)
\({Q_3}\) là trung vị của nửa số liệu \(45;{\rm{ }}48;\;71;72\). Do đó \({Q_3} = \frac{1}{2}(48 + 71) = 59,5\)
+) Chỉ có giá trị 41 xuất hiện 2 lần, nhiều hơn các giá trị còn lại.
Do đó mốt \({M_o} = 41\)
b) \(12;{\rm{ }}32;{\rm{ }}93;{\rm{ }}78;{\rm{ }}24;{\rm{ }}12;{\rm{ }}54;{\rm{ }}66;{\rm{ }}78\).
+) Số trung bình: \(\overline x = \frac{{12 + 32 + 93 + 78 + 24 + 12 + 54 + 66 + 78}}{9} \approx 49,89\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(12;{\rm{ }}12;{\rm{ }}24;{\rm{ }}32;{\rm{ }}54;{\rm{ }}66;{\rm{ }}78;{\rm{ }}78;\;93\)
Bước 2: \(n = 9\), là số lẻ nên \({Q_2} = {M_e} = 54\)
\({Q_1}\) là trung vị của nửa số liệu \(12;{\rm{ }}12;{\rm{ }}24;{\rm{ }}32\). Do đó \({Q_2} = \frac{1}{2}(12 + 24) = 18\)
\({Q_3}\) là trung vị của nửa số liệu \(66;{\rm{ }}78;{\rm{ }}78;\;93\). Do đó \({Q_3} = \frac{1}{2}(78 + 78) = 78\)
+) Giá trị 12 và giá trị 78 xuất hiện 2 lần, nhiều hơn các giá trị còn lại.
Do đó mốt \({M_o} = 12,{M_o} = 78.\)
cho phân số \(\dfrac{25}{37}\) . Hãy tìm một số tự nhiên sao cho khi đem mẫu số của phân số đó trừ đi số đó và giữ nguyên tử số ta được phân số mới có giá trị bằng \(\dfrac{5}{6}\)
Quy đồng tử số hai phân số \(\dfrac{25}{37}\) ta được hai phân số \(\dfrac{25}{37}\) và \(\dfrac{25}{30}\)
Số đó là : 37-30=7
Đáp số : 7
Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.

Tham khảo:
Ta có:

Số trung bình là \(\bar x = \frac{{3 \times 15 + 15 \times 45 + 10 \times 75 + 7 \times 105}}{{3 + 15 + 10 + 7}} = 63\)
Cỡ mẫu là: \(n = \;3\; + \;15\; + \;10\; + \;7\; = 35\)
Ý nghĩa: Xấp xỉ bằng số trung bình của mẫu số liệu gốc, cho biết vị trí trung tâm của mẫu số liệu và đại diện cho mẫu số liệu
Trung vị là \({x_{18}}\) thuộc nhóm \(\left[ {30;60} \right)\), do đó
\(p = 2,\;{a_2} = 30;\;{m_2} = 15;\;\;{m_1} = 3;\;\;{a_3} - {a_2} = 30\) và ta có:
\({M_e} = 30 + \frac{{\frac{{35}}{2} - 3}}{{15}} \times 30 = 59\).