Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - 4;1] \cap [0;3)\)
b) \((0;2] \cup (- 3;1]\)
c) \(( - 2;1] \cap (1;+ \infty )\)
d) \(\mathbb{R}{\rm{\backslash }}( - \infty ;3]\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;1) \cap (0; + \infty )\)
b) \((4;7] \cup ( - 1;5)\)
c) \((4;7]\;{\rm{\backslash }}\;( - 3;5]\)
Tham khảo:
a) Ta có:
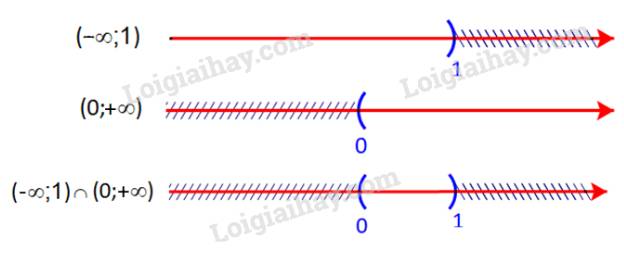
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:

Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
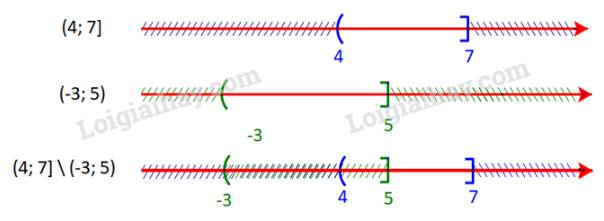
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: (4; 7) ∩ (-7; -4)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: [-3; 1) ∪ (0; 4]
[-3;1) = {x ∈ R| -3 ≤ x < 1} (0;4] = {x ∈ R| 0 < x ≤ 4} ⇒ [-3;1) ∪ (0;4] = {x ∈ R| -3 ≤ x < 1 hoặc 0 < x ≤ 4} = {x ∈ R| -3 ≤ x ≤ 4} = [-3;4] Biểu diễn [–3; 4] trên trục số:
Xác định các tập hợp sau và biểu diễn chúng trên trục số: (-12; 3] ∩ [-1; 4]
Xác định các tập hợp sau và biểu diễn chúng trên trục số
R \ ((3; 5) ∩ (4; 6))
R ( ( 3 ; 5 ) ∩ ( 4 ; 6 ) ) = ( - ∞ ; 4 ) ∪ [ 5 ; + ∞ )
Xác định các tập hợp sau và biểu diễn chúng trên trục số
((-1; 2) ∪ (3; 5)) \ (1; 4)
( ( - 1 ; 2 ) ∪ ( 3 ; 5 ) ) ( 1 ; 4 ) = ( - 1 ; 1 ] ∪ [ 4 ; 5 )
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (2; +∞)
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (-∞; 3]
Xác định các tập hợp sau và biểu diễn chúng trên trục số: R \ (2; +∞)