Em hãy viết tiếp các đường trung tuyến còn lại của tam giác ABC (Hình 1).
a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.
Em hãy quan sát vào cho biết:
- AD có phải đường trung tuyến của tam giác ABC hay không?
- Các tỉ số \(\dfrac{{BG}}{{BE}}\), \(\dfrac{{CG}}{{CF}}\), \(\dfrac{{AG}}{{AD}}\) bằng bao nhiêu?
Tham khảo:
a)
- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
- Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
- Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
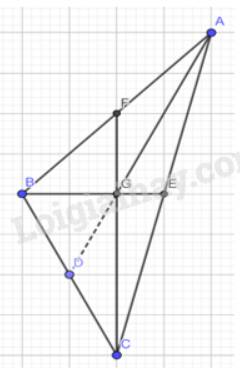
- Ta nối dài đoạn AG sao cho AG cắt BC tại 1 điểm
- Ta thấy điểm giao nhau giữa AG và BC chính là trung điểm của BC
- Nên AG là trung tuyến của tam giác ABC
- Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
\(\dfrac{{BG}}{{BE}} = \dfrac{2}{3};\dfrac{{CG}}{{CF}} = \dfrac{4}{6};\dfrac{{AG}}{{AD}} = \dfrac{{4.4}}{{6.6}}\)
- Ta thấy sau khi rút gọn các tỉ số ta có :
\(\dfrac{{BG}}{{BE}} = \dfrac{{CG}}{{CF}} = \dfrac{{AG}}{{AD}} = \dfrac{2}{3}\)
Cho tam giác ABC có đường trung tuyến CM, AN, BP cắt nhau tại G. Giả sử AB=3,2 ; CM=2,4 ; AN=1,8. Hãy tính
a, Đường cao GH của tam giác AGM
b, diện tích tam giác ABC
c, Tính độ dài đường trung tuyến còn lại của tam giác ABC
d, Tính độ dài cạnh còn lại của tam giác ABC
cho tam giác ABC có điểm A(3;9) và 2 đường trung tuyến (BM): 3x - 4y + 9 = 0, (CN): y - 6 = 0. Viết phương trình các cạnh còn lại của tam giác
Cho tam giác ABC vuông tại A có cạnh AB = 6cm, góc C = 60 độ. Hãy tính độ dài các cạnh còn lại và đường cao, đường trung tuyến hạ từ A của tam giác ABC
các bạn giải hộ mình :3
Cho tam giác ABC có A(2,,2) có phương trình đường trung tuyeensd1: 8x+y-7=0, d2: 10x-7y+5=0. Viết phương trình các cạnh và đường trung tuyến còn lại.
cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm, 3,6cm; cạnh BC=4cm. tính diện tích tam giác ABC và tính hai cạnh còn lại của tam giác ABC
cho tam giác ABC có các đường trung tuyến làAD:BE:CF chứng minh ba đường trung tuyến đó là 3 cạnh của 1 hình tam giác
Trên tia đối của DG, lấy điểm K sao cho DK=DG. Nối K với B. Ta được \(\Delta\)BGK với 3 cạnh BG,GK,BK.
AD là trung tuyến của \(\Delta\)ABC, G là trọng tâm của tam giác ABC \(\Rightarrow\)AG=2/3AD \(\Rightarrow\)DG=1/3AD.
DK=DG \(\Rightarrow\)DK=1/3 AD \(\Rightarrow\)DG+DK=1/3AD+1/3AD=2/3AD \(\Rightarrow\)GK=2/3 AD (1)
Ta có: BG là 1 cạnh của \(\Delta\)BGK và BG=2/3BE (2)
Xét \(\Delta\)CGD và \(\Delta\)BKD có:
CD=BD
\(\widehat{CDG}\)=\(\widehat{BDK}\) (Đối đỉnh) \(\Rightarrow\)\(\Delta\)CGD=\(\Delta\)BKD (c.g.c)
DG=DK
\(\Rightarrow\)CG=BK (2 cạnh tương ứng). Mà theo tính chất 3 đường trung tuyến của tam giác : CG=2/3 CF \(\Rightarrow\)BK=2/3CF (3)
Từ (1),(2) và (3) \(\Rightarrow\)3 đường trung tuyến AD,BE,CF tỉ lệ với 3 cạnh của \(\Delta\)BGK lần lượt là GK,BG,BK.
\(\Rightarrow\)AD,BE,CF thỏa mãn bất đẳng thức tam giác hay ta có thể nói AD,BE,CF là 3 cạnh của một hình tam giác (đpcm).
Gọi G là trọng tâm của tam giác ABC . Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.
Gọi G là trọng tâm của tam giác ABC . Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.