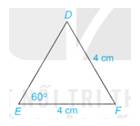
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.
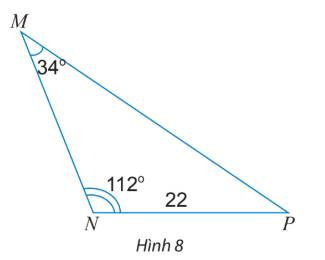
Ta có: \(NP = 22,\;\widehat P = {180^o} - ({112^o} + {34^o}) = {34^o}\)
Áp dụng định lí sin, ta có:
\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)
Suy ra:
\(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\)
\(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\)
Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.
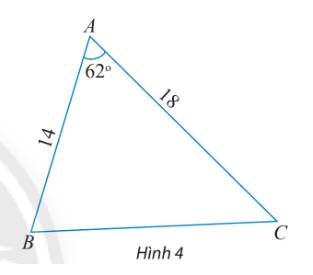
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45'\widehat C \approx {47^o}15'.\)
Cho △ABC=△DEF. Biết hai tia phân giác trong của góc B và góc C cắt nhau tại O tạo thành góc BOC có số đo bằng 135 độ và góc B=2 góc C Tính các góc của tam giác DEF.
cho tam giác abc đồng dạng tam giác def
biết Â=45 độ B = 55 độ
cạnh ab= 5cm :ac=7cm
BC=8cm ;EF=12cm
tính số đo các góc của tam giác DEF và độ dài DE ,DF
mọi người ơi ai bit lm hông chỉ tui zới
Giải
Vì\(\Delta ABC~\Delta DEF\) nên ta có:
\(\widehat{D}=\widehat{A}=45^o\)
\(\widehat{E}=\widehat{B}=55^o\)
\(\widehat{F}=\widehat{C}=\left(180^o-45^o-55^o\right)=80^o\)
Xét\(\Delta ABC~\Delta DEF\) có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{AB.3}{2}=7,5\)
\(DF=\frac{AC.3}{2}=10,5\)
#hoktot<3#
Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông.

a) Vì tổng 3 góc trong tam giác là \({180^o}\)
Nên ta có :
\(\begin{array}{l} \Rightarrow \widehat {DEC} + \widehat {DCE} + \widehat {CDE} = {180^o}\\ \Rightarrow \widehat {DCE} = {180^o} - \widehat {DEC} - \widehat {CDE}\\ \Rightarrow \widehat {DCE} = {180^o} - {58^o} - {32^o} = {90^o}\end{array}\)
b) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {HGF} + \widehat {GHF} + \widehat {GFH} = {180^o}\\ \Rightarrow \widehat {GFH} = {180^o} - \widehat {HGF} - \widehat {GHF}\\ \Rightarrow \widehat {GFH} = {180^o} - {68^o} - {42^o} = {70^o}\end{array}\)
c) Theo đề bài ta có :
\(\begin{array}{l} \Rightarrow \widehat {IJK} + \widehat {JKI} + \widehat {JIK} = {180^o}\\ \Rightarrow \widehat {JIK} = {180^o} - \widehat {IJK} - \widehat {JKI}\\ \Rightarrow \widehat {JIK} = {180^o} - {27^o} - {56^o} = {97^o}\end{array}\)
Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

a) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {180^o} - {72^o} - {44^o} = {64^o}\end{array}\)
b) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {180^o} - {59^o} - {31^o} = {90^o}\end{array}\)
c) Theo định lí về tổng số đo 3 góc trong tam giác ta có :
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {120^o} - {33^o} = {27^o}\end{array}\)
Cho △ABC=△DEF. Biết hai tia phân giác trong của góc B và góc C cắt nhau tại O tạo thành góc BOC có số đo bằng 135 độ và góc B=2 góc C Tính các góc của tam giác DEF.
Xét tam giác BOC có:
B1 + C1+ 135o = 180o
B1 +C1 = 45o
Ta có:
B= B1+ B2
C= C1+ C2
Và B +C +A = 180o
(B1+ B2)+ (C1+ C2) +A = 180o
2*B1 + 2*C1 +A = 180o
2* (B1+ C1) +A= 180o
2* 45o +A= 180o
90o +A= 180o
A= 90o
Ta có: B= 2C
và B +C +A = 180o
2C +C +90o =180o
3C = 90o
C = 30o
=> B= 2C = 2 * 30o= 60o
Mà tam giác ABC = tam giác DEF
=> A=D= 90o
E= B= 60o
C= F= 30o
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
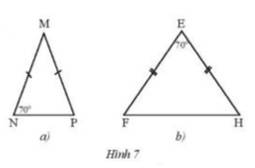
a) Vì \(\Delta MNP\) cân tại M ( theo giả thiết )
\( \Rightarrow \widehat N = \widehat P = {70^o}\) ( 2 góc đáy của tam giác cân )
\( \Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}\)
b) Xét \(\Delta EFH\) cân tại E
Theo định lí về tổng 3 góc trong tam giác ta có
\( \Rightarrow \widehat E + \widehat F + \widehat H = {180^o}\)
Mà \(\widehat F = \widehat H\)( tính chất tam giác cân )
\( \Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}\)
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

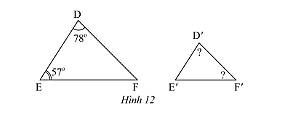
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).
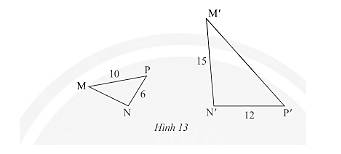
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).