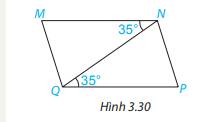
Cho Hình 3.30, biết các góc MNQ và PQN có cùng số đo bằng 35 \(^\circ \).
Chứng tỏ MN // QP.
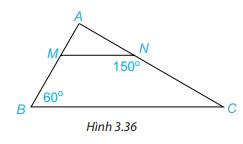
1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \).
Hãy tính số đo các góc BMN và ACB.
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không?

1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \)
Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\)
Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \).
2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong)
Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \)
Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.
Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.
a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)
b) \(\widehat P = \widehat Q = 110^\circ \)
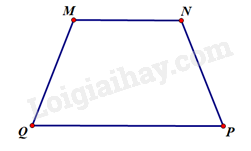
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)
betty vẽ một số tia xuất phát từ cùng một điểm và cùng nằm trên một nửa mặt phẳng . sau đó , bạn nhận thấy rằng trong các góc được tạo ra , có hai góc có số đo bằng $110^\circ$ , hai góc có số đo bằng $75^\circ$ và hai góc có số đo bằng $40^\circ$. hỏi betty đã vẽ ít nhất bao nhiêu tia ?
4 tia vì 2 + 2 = 4
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
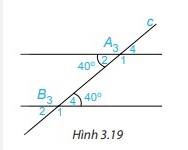
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
Cho hình vẽ bên. Chứng minh rằng:
a) MNQ =PQN;
b) MN song song với PQ ;
c) MQ song song với NP ; 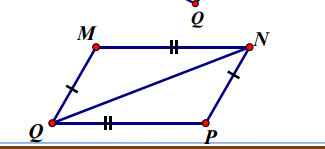
a) Xét \(\Delta MNQvà\Delta PQN\) ta có:
\(\left\{{}\begin{matrix}MN=PQ\\MQ=NP\\NQ:cạnhchung\end{matrix}\right.\)
\(\Rightarrow\Delta MNQ=\Delta PQN\)
Cho Hình 3.42, biết rằng Ax//Dy, \(\widehat A = 90^\circ ,\widehat {BCy} = 50^\circ \). Tính số đo các góc ADC và ABC.

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó, \(\widehat{ADC}=90^0\)
Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Vậy \(\widehat{ADC}=90^0; \widehat {ABC} = 50^\circ \)
Cho Hình 66 có \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\). Chứng minh MN = QP, MP = QN.
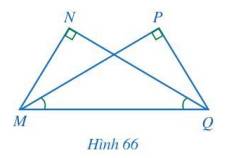
Ta có: tổng ba góc trong một tam giác bằng 180° và \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\) nên \(\widehat {PQM} = \widehat {NMQ}\).
Xét hai tam giác MNQ và QPM có:
\(\widehat {NQM}=\widehat {PMQ}\)
MQ chung
\(\widehat {NMQ}=\widehat {PQM}\)
Vậy \(\Delta MNQ = \Delta QPM\)(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)
Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60\(^\circ \)(\(\widehat {xAB} = \widehat {yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
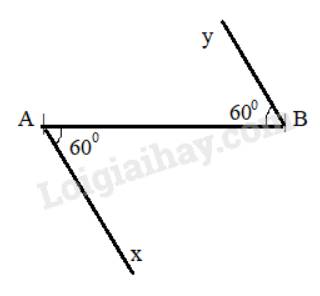
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
Bài 2. Vẽ góc xOy có số đo bằng 60 độ . Vẽ tia đối Ot của tia Ox, trên cùng một nửa mặt phẳng bờ xy chứa tia Oy vẽ tia Oz sao cho góc xOz có số đo bằng 120 độ . a) Tính số đo các góc yOz và góc zOt. b) Chứng tỏ: Oy là tia phân giác của góc xOz.
a) ta có xOz= xOy+ yOz=120 độ. Mà xOy = 60 độ
=> yOz = 60 độ
ta lại có xOy=180 ( Ot đối tia Ox)
=> tOz + xOz= xOy=180 độ
=> tOz= xOy-xOz=180 độ - 120 độ= 60 độ
b) Ta có xOy= yOz=60 độ( cmt)
=> Oy pg xOz