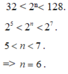Tìm số nguyên dương n biết : a) 32 < 2\(^n\)<128 ; b) 2.16 \(\ge\)2\(^n\)> 4 ; c) 9.27 \(\le\)3\(^n\)\(\le\)243
KD
Những câu hỏi liên quan
tìm số nguyên dương n biết rằng 32<2n<128
ta có 2^5<2^n<2^7
=>5<n<7
vì n là số nguyên dương
=>n=6
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết: 32 < 2n< 128
Tìm các số nguyên dương n biết: 32<2^n<128. ; b)32>2^n>4 ; c)9.27<3^n<243. Helpp!!!!!!
a.32<2n<128
25<2n<27
=> n=6
b.32>2n>4
25>2n>22
=> n=3; n=4
c. 9.27<3n<243
243<3n<243
35<3n<35
=> không tồn tại n
Đúng 0
Bình luận (0)
tìm số nguyên dương n biết rằng 32<2n<128
=2.16<2n<2.64
suy ra:16<n<64
các bạn làm nốt dùm mk nha!
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết rằng: 32<2n<128
32<2n<128
2x16<2n<2x64
=> 16<n<64
Mà n thuộc N nên n thuộc {17;18;19;...;63}
Đúng 0
Bình luận (0)
Tìm các số nguyên dương n, biết:
32<2^n<128 ; b)2.16>2^n>4; c)9.27<3^n<243
Tìm các số nguyên dương n biết: 32<\(2^n\)<128
Tìm số nguyên dương n, biết :
\(\left(\frac{1}{32}\right)^n.16^n=1024^{-1}\)
(1/32)n.16n=1024-1
=> (1/32.16)n=1/1024
=> (1/2)n=1/1024
=> (1/2)n=(1/2)10
=> n=10
Đúng 0
Bình luận (0)
\(\left(\frac{1}{32}\right)^n.16^n=1024^{-1}\)
\(\left(\frac{1}{32}.16\right)^n=\frac{1}{1024}\)
\(\left(\frac{1}{2}\right)^n=\frac{1}{1024}\)
\(\frac{1^n}{2^n}=\frac{1}{1024}\)
<=> 1n = 1 => n thuộc N
<=> 2n = 1024
=> 2n = 1024 = 210 ( 2n = 210 )
<=> n = 10
Đúng 0
Bình luận (0)
TÌM SỐ NGUYÊN DƯƠNG N BIẾT:
A) 32 < 2N <128 B )2 .16 BÉ HƠN BẰNG 2N >4 C)9.27 LỚN HƠN BẰNG 3N LỚN HƠN BẰNG 243
CHI NHA CAC BAN
bài 1 :
a) so sánh A và B biết : A 229 và B539
b) B 31+32+33+34+...+32010 chia hết cho 4 và 13
c) tính A 1-3+32-33+34-...+398-399+3100
bài 2 tìm cái số nguyên n thỏa mãn
a) tìm các số nguyên n sao cho 7 ⋮ (n+1)
b) tìm các số nguyên n sao cho (2n + 5 ) ⋮ (n+1)
Đọc tiếp
bài 1 :
a) so sánh A và B biết : A =229 và B=539
b) B = 31+32+33+34+...+32010 chia hết cho 4 và 13
c) tính A = 1-3+32-33+34-...+398-399+3100
bài 2 tìm cái số nguyên n thỏa mãn
a) tìm các số nguyên n sao cho 7 ⋮ (n+1)
b) tìm các số nguyên n sao cho (2n + 5 ) ⋮ (n+1)
Bài 1:
a. $2^{29}< 5^{29}< 5^{39}$
$\Rightarrow A< B$
b.
$B=(3^1+3^2)+(3^3+3^4)+(3^5+3^6)+...+(3^{2009}+3^{2010})$
$=3(1+3)+3^3(1+3)+3^5(1+3)+...+3^{2009}(1+3)$
$=(1+3)(3+3^3+3^5+...+3^{2009})$
$=4(3+3^3+3^5+...+3^{2009})\vdots 4$
Mặt khác:
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2008}+3^{2009}+3^{2010})$
$=3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2008}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+....+3^{2008})=13(3+3^4+...+3^{2008})\vdots 13$
Đúng 0
Bình luận (0)
Bài 1:
c.
$A=1-3+3^2-3^3+3^4-...+3^{98}-3^{99}+3^{100}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{99}-3^{100}+3^{101}$
$\Rightarrow A+3A=3^{101}+1$
$\Rightarrow 4A=3^{101}+1$
$\Rightarrow A=\frac{3^{101}+1}{4}$
Đúng 0
Bình luận (0)
Bài 2:
a. $7\vdots n+1$
$\Rightarrow n+1\in \left\{1; -1; 7; -7\right\}$
$\Rightarrow n\in \left\{0; -2; 6; -8\right\}$
b.
$2n+5\vdots n+1$
$\Rightarrow 2(n+1)+3\vdots n+1$
$\Rightarrow 3\vdots n+1$
$\Rightarrow n+1\in \left\{1; -1; 3; -3\right\}$
$\Rightarrow n\in \left\{0; -2; 2; -4\right\}$
Đúng 0
Bình luận (0)