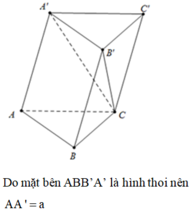
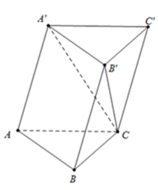
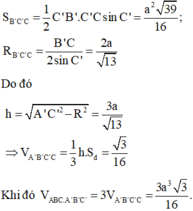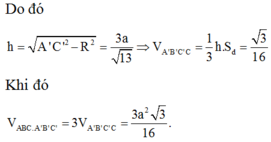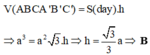Cho hình lăng trụ ABC.A'B'C' có các đáy là các tam giác đều. Tính góc (AB, B'C').
H24
Những câu hỏi liên quan
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh 2a, biết thể tích của khối lăng trụ ABC.ABC bằng
a
3
. Tính khoảng cách h giữa hai đường thẳng AB và BC.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a, biết thể tích của khối lăng trụ ABC.A'B'C' bằng a 3 . Tính khoảng cách h giữa hai đường thẳng AB và B'C'.
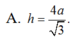
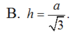
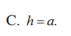
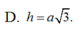
Cho hình lăng trụ tam giác
A
B
C
.
A
B
C
có đáy là tam giác đều cạnh a Cạnh bên tạo với đáy một góc
60
0
.
Gọi M là trung điểm của
B
C
và I là trung điểm của đoạn
A
M
. Biết hình chiếu vuông góc của I trên mặt phẳng đáy
A
B...
Đọc tiếp
Cho hình lăng trụ tam giác A B C . A ' B ' C ' có đáy là tam giác đều cạnh a Cạnh bên tạo với đáy một góc 60 0 . Gọi M là trung điểm của B ' C ' và I là trung điểm của đoạn A ' M . Biết hình chiếu vuông góc của I trên mặt phẳng đáy A B C là trọng tâm cả tam giác A B C . Tính thể tích của khối lăng trụ A B C . A ' B ' C ' theo
A. a 3 3 4 .
B. a 3 3 48 .
C. a 3 3 16 .
D. a 3 3 12 .
Cho lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a, mặt bên ABBA là hình thoi
A
A
C
^
60
∘
;
B
C
a
3
2
.
Tính thể tích khối lăng trụ ABC.ABC. A.
a...
Đọc tiếp
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, mặt bên ABB'A' là hình thoi A ' A C ^ = 60 ∘ ; B ' C = a 3 2 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. a 3 3 4
B. 3 a 3 3 16
C. a 3 3 16
D. 3 a 3 3 4
Cho lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a, mặt bên ABBA là hình thoi
A
A
C
⏜
60
0
; BC
a
3
2
.Tính thể tích khối lăng trụ ABC.ABC.
Đọc tiếp
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, mặt bên ABB'A' là hình thoi A A ' C ⏜ = 60 0 ; B'C= a 3 2 .Tính thể tích khối lăng trụ ABC.A'B'C'.
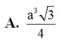
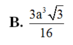
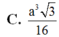
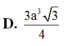
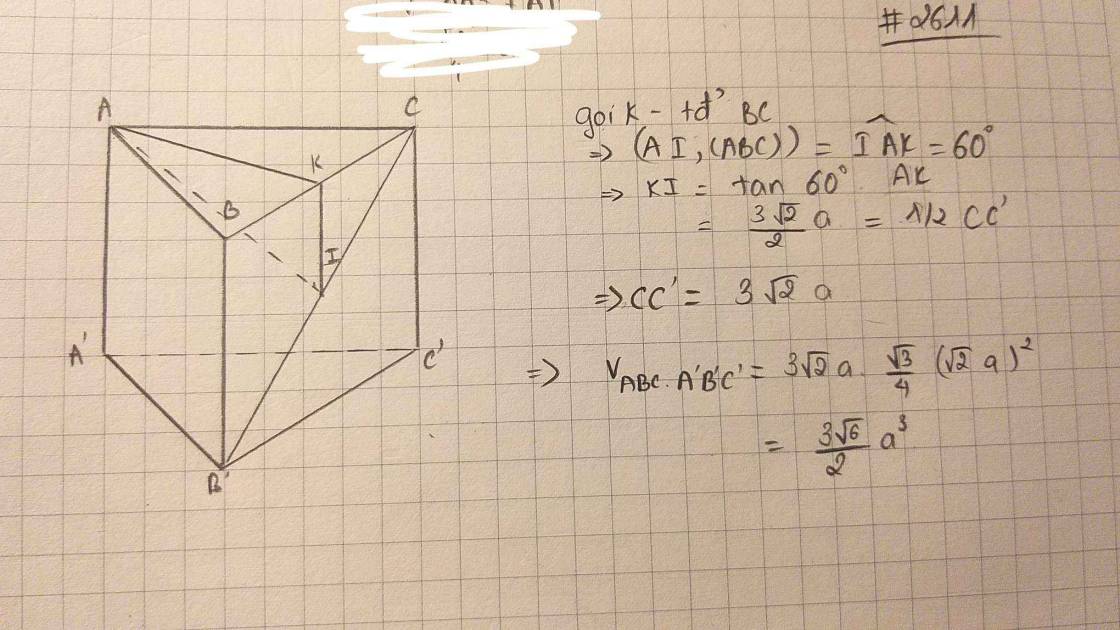
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a√2 . Gọi I là trung điểm B'C góc giữa AI và đáy bằng 60. Tính thể tích V của khối lăng trụ ABC. A'B'C' .
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy ABC là tam giác đều cạnh 2a. biết thể tích của khối lăng trụ
A
B
C
.
A
B
C
bằng
a
3
. Khoảng cách h giữa hai đường thẳng AB và BC bằng A.
4
a...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh 2a. biết thể tích của khối lăng trụ A B C . A ' B ' C ' bằng a 3 . Khoảng cách h giữa hai đường thẳng AB và B'C' bằng
A. 4 a 3
B. a 3
C. a
D. a 3
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A, ABa,
A
C
B
⏜
, bc tạo với mặt phẳng AABC một góc
30
0
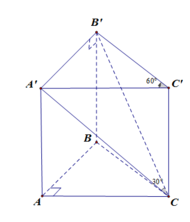
. Tính thể tích V của khối lăng trụ ABC.ABC.
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, A C B ⏜ , b'c tạo với mặt phẳng AA'B'C' một góc 30 0 . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
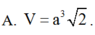

Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100).a) Tính góc giữa hai đường thẳng AB và BC.b) Tính góc giữa đường thẳng AB và mặt phẳng left( {ABC} right).c) Tính số đo của góc nhị diện left[ {B,CC,M} right].d) Chứng minh rằng CCparallel left( {ABBA} right). Tính khoảng cách giữa đường thẳng CC và mặt phẳng left( {ABBA} right).e) Chứng minh rằng CM bot left( {ABBA} right). Tính khoảng cách giữa hai đường thẳng CC và AM.g) Tính thể tích của k...
Đọc tiếp
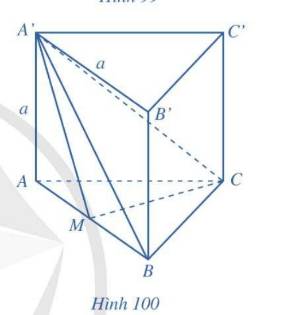
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(AB\) (Hình 100).
a) Tính góc giữa hai đường thẳng \(AB\) và \(B'C'\).
b) Tính góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {ABC} \right)\).
c) Tính số đo của góc nhị diện \(\left[ {B,CC',M} \right]\).
d) Chứng minh rằng \(CC'\parallel \left( {ABB'A'} \right)\). Tính khoảng cách giữa đường thẳng \(CC'\) và mặt phẳng \(\left( {ABB'A'} \right)\).
e) Chứng minh rằng \(CM \bot \left( {ABB'A'} \right)\). Tính khoảng cách giữa hai đường thẳng \(CC'\) và \(A'M\).
g) Tính thể tích của khối lăng trụ tam giác đều \(ABC.A'B'C'\) và thể tích khối chóp \(A'.MBC\).
a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)
Đúng 0
Bình luận (0)
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy là tam giác vuông cân tại
A
,
A
B
a
.
Biết thể tích của khối lăng trụ
A
B
C
.
A
B
C
là
V
4
a
3...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy là tam giác vuông cân tại A , A B = a . Biết thể tích của khối lăng trụ A B C . A ' B ' C ' là V = 4 a 3 3 . Tính khoảng cách giữa hai đường thẳng AB và B ' C '
A. h = 8 a 3
B. h = 3 a 8
C. h = 2 a 3
D. h = a 3
Đáp án A
Diện tích tam giác ABC là S A B C = 1 2 A B 2 = a 2 2
Chiều cao của khối lăng trụ là V A B C . A ' B ' C ' = S A B C × h ⇒ h = 8 a 3
Ta có B C / / B ' C ' ⇒ d A B ; B ' C ' = d B ' C ' ; A B C = d B ' ; A B C = h = 8 a 3
Đúng 0
Bình luận (0)