My có 9 tấm thẻ như dưới đây:
40581302
Từ các thẻ trên:
a) Hãy lập số lớn nhất
có 9 chữ số.
Rô bốt có 9 tấm thẻ như sau:

Từ các tấm thẻ trên:
a) Hãy lập số lớn nhất có chín chữ số
b) Hãy lập số bé nhất có chín chữ số
Ta thấy: 0 < 1 < 3 < 7 < 8 < 9
Do đó, từ các tấm thẻ trên, ta lập được:
a) Số lớn nhất có 9 chữ số: 988 731 000
b) Số bé nhất có 9 chữ số: 100 037 889
Trên bản có các tấm thẻ ghép được thành số 1 951 890

a) Lấy ra một tấm thẻ để được số có sáu chữ số lớn nhất có thể
b) Lấy ra một tấm thẻ để được số có sáu chữ số bé nhất có thể
a) Lấy ra tấm thẻ số 0. Ta được số có sáu chữ số lớn nhất có thể là: 998 511
b) Lấy ra tấm thẻ số 9. Ta được số có sáu chữ số bé nhất có thể là: 101 589
Một hộp đứng 9 tấm thẻ được đánh số từ 1 đến 9. Hỏi phải rút ít nhất bao nhiêu thẻ để xác suất
có ít nhất một thẻ ghi số chia hết cho 4 phải lớn hơn 5 6 ?
A. 4
B. 5
C. 6
D. 7
Chọn đáp án C
Cách 1: Gọi P n A là xác suất rút ít nhất được một thẻ ghi số chia hết cho 4 từ n lần rút.
Gọi P n B là xác suất không rút được thẻ ghi số chia hết cho 4 từ n lần rút.


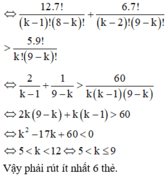
Một hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Hỏi phải rút ít nhất bao nhiêu thẻ để xác suất “có ít nhất một thẻ ghi số chia hết cho 4” phải lớn hơn 5 6
A. 7
B. 6
C. 5.
D. 4
Một hộp có 100 tấm thẻ như nhau ñược ghi các số từ 1 ñến 100, Rút ngẫu nhiên hai thẻ rồi ñặt theo thứ tự từ trái qua phải. Tính xác suất ñển a/ Rút ñược hai thẻ lập nên một số có hai chữ số. b/ Rút ñược hai thẻ lập nên một số chia hết cho 5.
Một hộp có chứa 7 quả cầu trắng và 3 quả cầu ñen cùng kích thước. Rút ngẫu nhiên cùng một lúc 4 quả cầu. Tính xác suất ñể trong 4 quả cầu rút ñược có a/ Hai quả cầu ñen. b/ Ít nhất 2 cầu ñen c/ Toàn cầu trắng
Một hộp thuốc có 5 ống thuốc tốt và 3 ống kém chất lượng. Chọn ngẫu nhiên lần lượt không trả lại 2 ống. Tính xác suất ñể: a/ Cả hai ống ñược chọn ñều tốt. b/ Chỉ ống ñược chọn ra ñầu tiên là tốt. c/ trong hai ống có ít nhất một ống thuốc tốt.
Trò chơi Ai lấy được nhiều thẻ mang số chẵn nhất?
Trò chơi dành cho một nhóm bạn.
Có 10 tấm thẻ như dưới đây, các tấm thẻ được lật úp trên bàn.

Các bạn lần lượt thay nhau, mỗi lần lấy một tấm thẻ.
- Nếu tấm thẻ mang số chẵn thì bạn đó được vẽ một vạch vào bảng con của mình.
- Sau đó, thẻ được lật úp và để lại bàn.
Sau khi mỗi bạn thực hiện 10 lần lấy thẻ, cả nhóm thống kê xem ai lấy được nhiều lần thẻ mang số chẵn nhất.
Học sinh tự thực hiện
Có 9 tấm thẻ đánh số từ 1 đến 9. Chọn ngẫu nhiên ra hai tấm thẻ. Tính xác suất để tích của hai số trên hai tấm thẻ là một số chẵn.
A. 13 18
B. 55 56
C. 5 28
D. 1 56
Có 9 tấm thẻ đánh số từ 1 đến 9. Chọn ngẫu nhiên ra hai tấm thẻ. Tính xác suất để tích của hai số trên hai tấm thẻ là một số chẵn
A. 13 18 .
B. 55 56 .
C. 5 28 .
D. 1 56 .
Chọn A.
Lấy ngẫu nhiên tấm thẻ từ 9 tấm thẻ có C 9 2 = 36 cách => số phần tử của không gian mẫu là n Ω = 36 .
Gọi A: “tích của hai số trên tấm thẻ là một số chẵn”.
Để tích của hai số trên tấm thẻ là một số chẵn thì ít nhất một trong hai tấm thẻ phải là số chẵn. Ta có hai trường hợp
TH1: Cả hai thẻ được lấy ra đều là số chẵn có C 4 2 = 6 cách.
Th2: Hai thẻ lấy ra có một thẻ là số chẵn, một thẻ là số lẻ C 4 1 . C 5 1 = 20 cách.
Số kết quả thuận lợi cho A là n(A) = 6 + 20 = 26.
Vậy xác suất của biến cố A là P A = n A n Ω = 13 18 .
Có ba tấm thẻ ghi số 1, một tấm thẻ ghi số 5, một tấm thẻ ghi số 7, một tấm thẻ ghi số 8. Hỏi có thể lập được bao nhiêu số tự nhiên có sáu chữ số khi đặt sáu tấm thẻ này trên cùng một hàng?