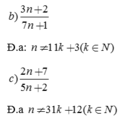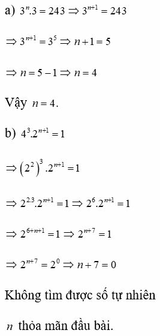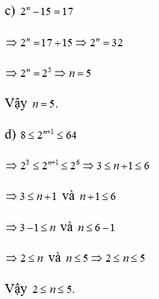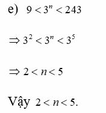tìm n a)1: 9. 27n=3n
HN
Những câu hỏi liên quan
Tìm các số tự nhiên n để các phân số sau là phân số tối giản:a)
2
n
+
3
4
n
+
1
b)
3
n
+
2
7
n
+
1
c)
2...
Đọc tiếp
Tìm các số tự nhiên n để các phân số sau là phân số tối giản:
a) 2 n + 3 4 n + 1
b) 3 n + 2 7 n + 1
c) 2 n + 7 5 n + 2
a)2n+3 chia hết n-2
b)3n+23 chia hết n+4
c)27n-5 chia hết n
d)3n+1 chia hết 11-2n
tim n
81<(1/9)*27n<3^10
m=1+3+3^2+3^3+...+3^2019
a) M là số nguyên tố hay hợp số
b) tìm số dư trong phép chia M cho 13
c) cm M chia hết 40
d) tìm số tự nhiên n dể 18m+9=27n
Tìm STN n để:
b) 19⋮ (n+2)
a) (3n-15)⋮ n
c) (n+9) ⋮ (n+1)
d) (3n+21) ⋮ (n+1)
e) (n+8) ⋮ (n-2)
f) (n2 + 4n +11) ⋮ (n+4)
b) \(\Rightarrow\left(n+2\right)\inƯ\left(19\right)=\left\{-19;-1;1;19\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{17\right\}\)
a) Do \(n\in N\)
\(\Rightarrow n\inƯ\left(15\right)=\left\{1;3;5;15\right\}\)
c) \(\Rightarrow\left(n+1\right)+8⋮\left(n+1\right)\)
Do \(n\in N\Rightarrow n\inƯ\left(8\right)=\left\{1;2;4;8\right\}\)
d) \(\Rightarrow3\left(n+1\right)+18⋮\left(n+1\right)\)
Do \(n\in N\Rightarrow\left(n+1\right)\inƯ\left(18\right)=\left\{1;2;3;6;9;18\right\}\)
\(\Rightarrow n\in\left\{0;1;2;5;8;17\right\}\)
e) \(\Rightarrow\left(n-2\right)+10⋮\left(n-2\right)\)
Do \(n\in N\Rightarrow\left(n-2\right)\inƯ\left(10\right)=\left\{-2;-1;1;2;5;10\right\}\)
\(\Rightarrow n\in\left\{0;1;3;4;7;12\right\}\)
f) \(\Rightarrow n\left(n+4\right)+11⋮\left(n+4\right)\)
Do \(n\in N\Rightarrow\left(n+4\right)\inƯ\left(11\right)=\left\{11\right\}\)
\(\Rightarrow n\in\left\{7\right\}\)
Đúng 3
Bình luận (1)
\(19:\left(n+2\right)\)
⇒ (n+2)∈Ư(19)=(1,19)
n+2 1 19
n -1(L) 17(TM)
Đúng 0
Bình luận (0)
Tìm n, biết:a,
3
n
.
3
243
b,
4
3
.
2
n
+
1
1
c,
2...
Đọc tiếp
Tìm n, biết:
a, 3 n . 3 = 243
b, 4 3 . 2 n + 1 = 1
c, 2 n - 15 = 17
d, 8 ≤ 2 n + 1 ≤ 64
e, 9 < 3 n < 243
a, 3 n . 3 = 243 => 3 n + 1 = 243 => 3 n + 1 = 3 5
=> n + 1 = 5 => n = 4
Vậy n = 4
b, 4 3 . 2 n + 1 = 1
=> 2 2 3 . 2 n + 1 = 1
=> 2 2 . 3 . 2 n + 1 = 1 => 2 6 . 2 n + 1 = 1
=> 2 6 + n + 1 = 1 => 2 n + 7 = 2 0
=> n + 7 = 0
Không tìm được số tự nhiên n thỏa mãn đầu bài
c, 2 n - 15 = 17
=> 2 n = 32 => 2 n = 2 5
=> n = 5
Vậy n = 5
d, 8 ≤ 2 n + 1 ≤ 64
=> 2 3 ≤ 2 n + 1 ≤ 2 6
=> 3 ≤ n + 1 và n+1 ≤ 6
=> 2 ≤ n và n ≤ 5
=> 2 ≤ n ≤ 5
Vậy 2 ≤ n ≤ 5
e, 9 < 3 n < 243
=> 3 2 < 3 n < 3 5
=> 2<n<5
Vậy 2<n<5
Đúng 0
Bình luận (0)
Tìm n, biết: a)
3
n
.
3
243
b)
4
3
.
2
n
+
1
1
c)
2
n
-
15
17
d)
8
≤
2
n
+
1...
Đọc tiếp
Tìm n, biết:
a) 3 n . 3 = 243
b) 4 3 . 2 n + 1 = 1
c) 2 n - 15 = 17
d) 8 ≤ 2 n + 1 ≤ 64
e) 9 < 3 n < 243
Chứng minh các đẳng thức sau (với n∈N∗n∈N∗)
a) 2+5+8+...+(3n−1)=n(3n+1)22+5+8+...+(3n−1)=n(3n+1)2;
b) 3+9+27+...+3n=12(3n+1−3)3+9+27+...+3n=12(3n+1−3).
tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)
Đúng 0
Bình luận (0)
Tìm số tự nhiên \(n\) \(\left(20349< n< 47238\right)\) và \(A\) để \(A=4789655-27n\) là lập phương của một số tự nhiên.