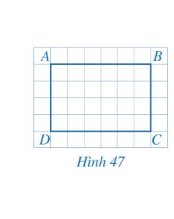
Cho biết số đo mỗi góc của tứ giác ABCD ở Hình 47.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
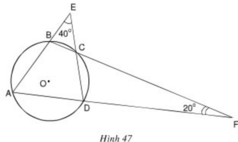
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
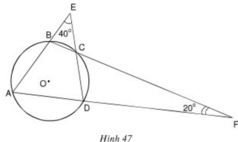
Ta có: B C E ^ = D C F ^ (hai góc đối đỉnh)
Đặt x = B C E ^ = D C F ^ . Theotinhs chất góc ngoài tam giác, ta có:
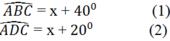
Lại có: ![]()
(Hai hóc đối điện tứ giác nội tiếp).
Từ (1),(2),(3) suy ra:
![]()
Từ (1), ta có: A B C ^ = 60 o + 40 o = 100 o
Từ (2), ta có: A D C ^ = 60 o + 20 o = 80 o
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
Bài 3:
a. Tính các góc của tứ giác ABCD bt số đo của chúng tương ứng với tỉ lệ với 2;2;1;1
b. Tứ giác ABCD cho ở câu a là hình gì? Vì sao?
( vẽ hình nữa nha)
a, Ta có \(\widehat{A}:\widehat{B}:\widehat{C}:\widehat{D}=2:2:1:1\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}\) và \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+1+2+2}=\dfrac{360^0}{6}=60^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=120^0\\\widehat{B}=120^0\\\widehat{C}=60^0\\\widehat{D}=60^0\end{matrix}\right.\)
b, Vì \(\widehat{A}+\widehat{C}=120^0+60^0=180^0\) mà 2 góc này ở vị trí TCP nên AB//CD
Do đó ABCD là hình thang
Vì \(\widehat{A}=\widehat{B}=120^0\) nên ABCD là hình thang cân
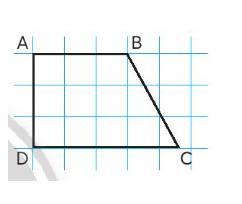
Cho hình tứ giác ABCD (xem hình bên).
a) Số đo mỗi góc của hình tứ giác là bao nhiêu độ?
b) Nêu tên các cặp cạnh vuông góc với nhau.
c) Nêu tên cặp cạnh song song với nhau.
a) Góc đỉnh A, cạnh AB, AD có số đo là 90o
Góc đỉnh D, cạnh DA, DC có số đo là 90o
Góc đỉnh B, cạnh BA, BC có số đo là 120o
Góc đỉnh C, cạnh CB, CD có số đo là 60o
b) AB và AD là cặp cạnh vuông góc với nhau
DA và DC là cặp cạnh vuông góc với nhau
c) AB và DC là cặp cạnh song song với nhau
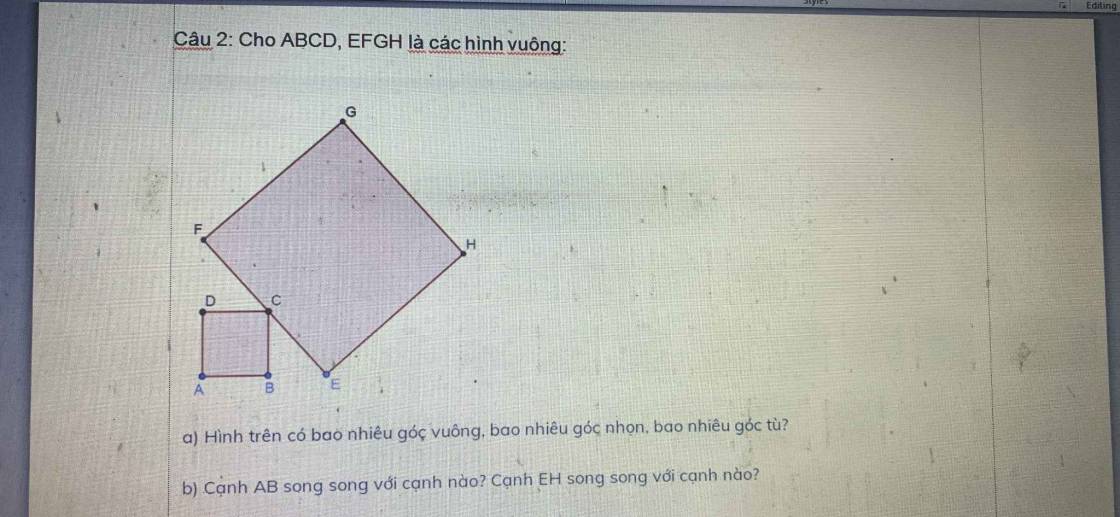 đó xem có ai giải được hông
đó xem có ai giải được hông
sốt ruột
Cho tứ giác ABCD biết số đo của các góc A, B, C, D tỉ lệ thuận với 1,2,3,4.
Tính số đo của các góc trong tứ giác ABCD.
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
Cho tứ giác ABCD có góc A = góc B = 90 độ
1) Chứng minh tứ giác ABCD là hình thang
Cho biết góc C = 3D Tính số đo góc C góc D
Cho tứ giác ABCD có A = 2B, B = 2D, C = 3/2D. Tính số đo mỗi góc của tứ giác ABCD.
Bài 1: Cho tứ giác ABCD biết số đo của các góc A; B; C; D tỉ lệ thuận với 5; 8; 13 và 10.
a/ Tính số đo các góc của tứ giác ABCD
b/ Kéo dài hai cạnh AB và DC cắt nhau ở E, kéo dài hai cạnh AD và BC cắt nhau ở F. Hai tia phân giác của các góc AED và góc AFB cắt nhau ở O. Phân giác của góc AFB cắt các cạnh CD và AB tại M và N. Chứng minh O là trung điểm của đoạn MN.
Bài 1: Cho tứ giác ABCD biết số đo của các góc A; B; C; D tỉ lệ thuận với 5; 8; 13 và 10.
a/ Tính số đo các góc của tứ giác ABCD
b/ Kéo dài hai cạnh AB và DC cắt nhau ở E, kéo dài hai cạnh AD và BC cắt nhau ở F. Hai tia phân giác của các góc AED và góc AFB cắt nhau ở O. Phân giác của góc AFB cắt các cạnh CD và AB tại M và N. Chứng minh O là trung điểm của đoạn MN.