Cho tam giác đều ABC . Gọi M ,N là hai điểm lần lượt trên hai cạnh AB , AC ; D là trung điểm BC
Biết chu vi tam giác AMN bằng nửa chu vi tam giác ABC , Tính góc MDN
Giúp mình vs ^^
H24
Những câu hỏi liên quan
GD
1 tháng 3 2021 lúc 20:06
Cho tam giác đều ABC. Trên cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = CN. Gọi O là giao điểm của CM và BN. Chứng minh rằng: a) CM = BN b) Góc BOC không đổi khi M và N di động trên hai cạnh AB, AC thỏa mãn AM=CN.
Xem chi tiết
a) Chứng minh CM=BN :AM = CN (gt)AC = BC ( cạnh tam giác đều)CAM^ = BCN^ = 60*=> Δ ACM = Δ CBN (c.g.c)=> CM = BN
b) Chứng minh góc BOC không đổi khi M và N di động trên hai cạnh AB và AC thỏa mãn AM=CNΔ ACM = Δ CBN => ACM^ = CBN^ => ABN^ = BCM^=> CBN^ + BCM^ = CBN^ + ABN^ = ABC^ = 60*=> BOC^ = 180* - (CBN^ + BCM^) = 180* - 60* = 120* không đổi
Đúng 1
Bình luận (4)
Cho tam giác ABC đều cạnh 1. Lấy điểm D ngoài tam giác ABC sao cho tam giác DBC cân tại D và góc BDC bằng 120 độ. Gọi M, N lần lượt là hai điểm trên các cạnh AB và AC sao cho góc MDN bằng 60 độ. Hãy tính chu vi của tam giác AMN.
Bạn có lời giải bài này chưa?? Có gửi mk với!
Đúng 0
Bình luận (0)
Bạn có lời giải bài này chưa? Có thì gửi cho mk với!!!
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Trên cạnh AB,AC lần lượt lấy điểm M,N sao cho AM=CN. Gọi O là giao điểm BN va CM.?
a) Chứng minh CM=BN
b) Chứng minh góc BOC không đổi khi M và N di động trên hai cạnh AB và AC thỏa mãn AM=CN
AM = CN (gt)
AC = BC ( cạnh tam giác đều)
CAM^ = BCN^ = 60*
=> Δ ACM = Δ CBN (c.g.c)
=> CM = BN
b) Chứng minh góc BOC không đổi khi M và N di động trên hai cạnh AB và AC thỏa mãn AM=CN
Δ ACM = Δ CBN => ACM^ = CBN^ => ABN^ = BCM^
=> CBN^ + BCM^ = CBN^ + ABN^ = ABC^ = 60*
=> BOC^ = 180* - (CBN^ + BCM^) = 180* - 60* = 120* không đổi
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB AC, gọi D là trung điểm của BC.a) Chứng minh :tam giác ABC tam giác ABD từ đó suy ra AD là tia phân giác của góc BACb) Chứng minh : AD vuông góc BCc) Trên cạnh AB và cạnh AC lần lượt lấy hai điểm M,N sao cho AMAN. Gọi K là giao điểm của AD và MN. Chứng minh AD vuông góc với MNd) Gọi O là trung điểm của BM, trên tia đối của tia OD lấy điểm P sao cho ODOP.Chứng minh rằng : ba điểm M,N,P thẳng hàng
Đọc tiếp
Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC.
a) Chứng minh :tam giác ABC = tam giác ABD từ đó suy ra AD là tia phân giác của góc BAC
b) Chứng minh : AD vuông góc BC
c) Trên cạnh AB và cạnh AC lần lượt lấy hai điểm M,N sao cho AM=AN. Gọi K là giao điểm của AD và MN. Chứng minh AD vuông góc với MN
d) Gọi O là trung điểm của BM, trên tia đối của tia OD lấy điểm P sao cho OD=OP.
Chứng minh rằng : ba điểm M,N,P thẳng hàng
Trong không gian cho hai tam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AC, CB, BC’, C’A. Tứ giác MNPQ là hình gì? A. Hình bình hành B. Hình chữ nhật C. Hình vuông D. Hình thang
Đọc tiếp
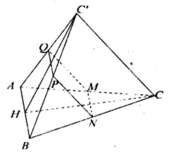
Trong không gian cho hai tam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AC, CB, BC’, C’A. Tứ giác MNPQ là hình gì?
A. Hình bình hành
B. Hình chữ nhật
C. Hình vuông
D. Hình thang
Đáp án B
Hướng dẫn giải: Dễ thấy tứ giác MNPQ là hình bình hành, gọi H là trung điểm của AB.
Vì hai tam giác đều ABC và ABC’ có chung cạnh AB nên
C H ⊥ A B C ' H ⊥ A B
Suy ra A B ⊥ ( C H C ' )
Do đó A B ⊥ C C '
Ta lại có:
Kết luận tứ giác MNPQ là hình chữ nhật
Đúng 0
Bình luận (0)
cho tam giác ABC đều. Trên 2 cạnh AB và AC lần lượt lấy hai điểm M , N sao cho AM=CN. Gọi O là giao điểm của CM và BN. Chứng minh rằng :
a) CM=BN
b) Số đo của góc BOC không đổi khi M và N di động trên hai cạnh AB, AC thỏa mãn điều kiện AM=CN
Cho tam giác đều ABC. Trên hai cạnh AB, AC lần lượt lấy hai điểm M, N sao cho AM=CN. Gọi O là giao điểm của CM và BN. Chứng minh rằng:
a, CM=BN
b, Số đo góc BOC không đổi khi M và N di động trên hai cạnh AB, AC thỏa mãn điều kiện AM=CN
Giải nhanh hộ mình nha!
Cho tam giác ABC có AB > AC > BC. trên các cạnh AB, AC lấy lần lượt hai điểm M và N Sao cho BM = BC = CN. Gọi I là tâm đường tròn nội tiếp tam giác ABC. AI cắt đường tròn ngoại tiếp các tam giác ANM và ABC lần lượt tại E và F.
a) Chứng minh tứ giác AMIC nội tiếp.
b) So sánh IE và IF
1. Cho tam giác ABC. Điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao choBD CE. Gọi I, K, M, N theo thứ tự là trung điểm của BE, CD, BC, DE.a. Tứ giác MINK là hình gì? Vì sao?b. Chứng minh rằng IK vuông góc với tia phân giác At của góc A.2. Cho tam giác đều ABC. Từ một điểm M trên cạnh AB vẽ hai đường thẳngsong song với hai cạnh AC, BC, chúng lần lượt cắt BC, AC tại D và E. Tìm vị trí củaM trên cạnh AB để độ dài đoạn DE đạt giá trị nhỏ nhất.
Đọc tiếp
1. Cho tam giác ABC. Điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho
BD = CE. Gọi I, K, M, N theo thứ tự là trung điểm của BE, CD, BC, DE.
a. Tứ giác MINK là hình gì? Vì sao?
b. Chứng minh rằng IK vuông góc với tia phân giác At của góc A.
2. Cho tam giác đều ABC. Từ một điểm M trên cạnh AB vẽ hai đường thẳng
song song với hai cạnh AC, BC, chúng lần lượt cắt BC, AC tại D và E. Tìm vị trí của
M trên cạnh AB để độ dài đoạn DE đạt giá trị nhỏ nhất.