Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.
H24
Những câu hỏi liên quan
Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc α, β.
b) Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc α, β.
Xem hình 37.
Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc α, β.
Xem hình 37.
Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc α, β.
b = asin α = acosβ; c = asinβ = acosα
Đúng 0
Bình luận (0)
Cho hình 37.
Hãy viết hệ thức giữa các tỉ số lượng giác của góc α và các tỉ số lượng giác của góc β.
sin α = cos β; cos α = sin β
tg α = cotg β; cotg α = tgβ
Đúng 0
Bình luận (0)
Cho hai góc
α
và
β
với
α
+
β
90
°
. Tính giá trị của biểu thức
P
cos
α
cos
β
−
sin
β
sin
α
. A.P 0 B. P 1 C. P -1 D. P 2
Đọc tiếp
Cho hai góc α và β với α + β = 90 ° . Tính giá trị của biểu thức P = cos α cos β − sin β sin α .
A.P = 0
B. P = 1
C. P = -1
D. P = 2
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = cos α cos β − sin β sin α = cos α sin α − cos α sin α = 0 .
Chọn A.
Đúng 0
Bình luận (0)
Cho hai góc
α
và
β
với
α
+
β
180
°
. Tính giá trị của biểu thức
P
cos
α
cos
β
−
sin
β
sin
α
. A.P 0 B. P 1 C . P -1 D. P 2
Đọc tiếp
Cho hai góc α và β với α + β = 180 ° . Tính giá trị của biểu thức P = cos α cos β − sin β sin α .
A.P = 0
B. P = 1
C . P = -1
D. P = 2
Hai góc α và β bù nhau nên sin α = sin β ; cos α = − cos β .
Do đó P = cos α cos β − sin β sin α = − cos 2 α − sin 2 α = − sin 2 α + cos 2 α = − 1 .
Chọn C.
Đúng 0
Bình luận (0)
Cho hai góc
α
và
β
với
α
+
β
90
°
. Tính giá trị của biểu thức
P
sin
α
cos
β
+
sin
β
cos
α
. A.P 0 B. P 1 C.P -1 D. P 2
Đọc tiếp
Cho hai góc α và β với α + β = 90 ° . Tính giá trị của biểu thức P = sin α cos β + sin β cos α .
A.P = 0
B. P = 1
C.P = -1
D. P = 2
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = sin α cos β + sin β cos α = sin 2 α + cos 2 α = 1 .
Chọn B.
Đúng 0
Bình luận (0)
Cho hình 19. Hãy cho biết tổng số đo của góc α và góc β. Lập các tỉ số lượng giác của góc α và góc β. Trong cặp tỉ số này, hãy cho biết các cặp tỉ số bằng nhau.
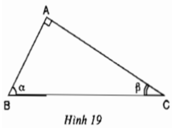
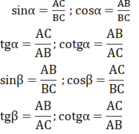
⇒ sinα = cosβ
cosα = sinβ
tgα = cotgα
cotgα = tgβ
Đúng 0
Bình luận (0)
Cho hình 19. Hãy cho biết tổng số đo của góc α và góc β. Lập các tỉ số lượng giác của góc α và góc β. Trong cặp tỉ số này, hãy cho biết các cặp tỉ số bằng nhau.
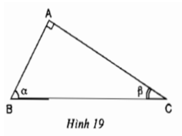
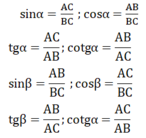
⇒ sinα = cosβ
cosα = sinβ
tgα = cotgα
cotgα = tgβ
Đúng 0
Bình luận (0)

