Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
H24
Những câu hỏi liên quan
Trong Ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN).
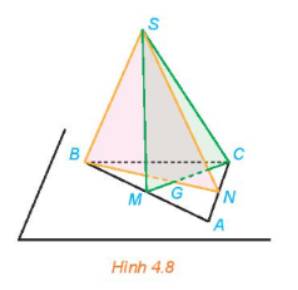
Vì A là giao điểm của BM và CN nên A nằm trên cả hai mặt phẳng (SBM) và (SCN).
Ta có: S, A là hai điểm chung của hai mặt phẳng (SBM) và (SCN) nên giao tuyến của hai mặt phẳng này là đường SA.
Đúng 0
Bình luận (0)
Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
Hai mp(SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song AD và BC.
Do đó, giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC.
Đúng 0
Bình luận (0)
Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).
Gọi O là giao điểm của AC và BD
Vì S và O cùng thuộc hai mặt phẳng (SAC) và (SBD)
Suy ra SO là giao tuyến của hai mặt phẳng (SAC) và (SBD)
Đúng 0
Bình luận (0)
Ví dụ 2: Cho tử diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AC. Trên cạnh DB lấy điểm P sao cho DP = 2PB . a). Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (ABD),(BCD).
Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.
Mặt phẳng (ABC) chứa đường thẳng AB song song với (Q) nên mp(ABC) cắt mp(Q) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc BC) thì EF là giao tuyến của (Q) và (ABC).
Hai mặt phẳng (ACD) và (ABD) cùng chứa đường thẳng AD song song với (Q) nên chúng cắt mặt phẳng (Q) theo giao tuyến song song với với AD. Vẽ EK song song với AD (K thuộc CD) thì EK, FK lần lượt là giao tuyến của mp(Q) với hai mp(ACD) và (BCD).
Đúng 0
Bình luận (0)
Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC).
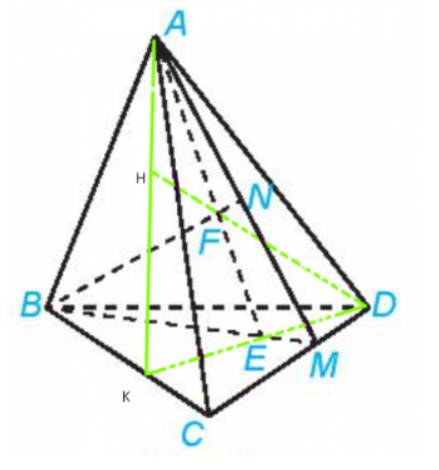
Xét trong mp(BCD) ta có: DE cắt BC tại K.
Xét trong mp(ADK) ta có: AF cắt AK tại H.
Như vậy, H thuộc đường thẳng DF và AK mà AK nằm trong mp(ABC) suy ra H cũng nằm trong mp(ABC).
Do đó, H là giao điểm của DF và mp(ABC).
Đúng 0
Bình luận (0)
Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp (S, a) và mp (S, c); mp (S, b) và mp (S, c).
Đường thẳng c cắt a, b lần lượng tại A và B.
Giao tuyến của mp(S,a) và mp(S,c) là SA.
Giao tuyến của mp(S,b) và mp(S,c) là SB.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
a) Hãy xác định điểm L.
b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD.
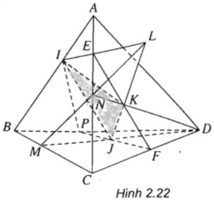
a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)
Đúng 0
Bình luận (0)
Với giả thiết như ở Ví dụ 3, chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
b) Giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
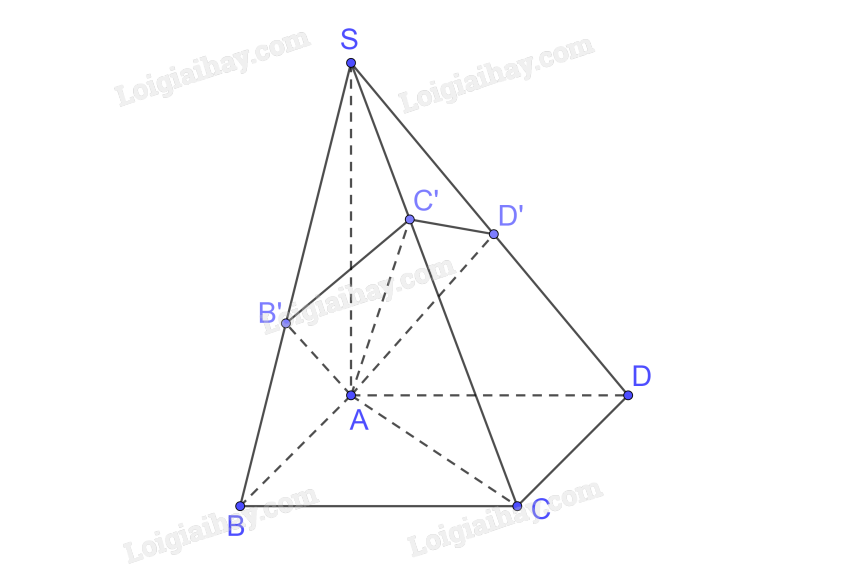
a) Từ ví dụ 3b ta có AB’, AC’ cùng đi qua A và vuông góc với SC
\( \Rightarrow SC \bot \left( {AB'C'D'} \right),SC \subset \left( {SAC} \right) \Rightarrow \left( {AB'C'D'} \right) \bot \left( {SAC} \right)\)
Ta có \(SA \bot \left( {ABCD} \right),SA \subset \left( {SAC} \right) \Rightarrow \left( {ABCD} \right) \bot \left( {SAC} \right)\)
Do đó các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC).
b) Vì (AB'C'D') và (ABCD) cùng vuông góc với (SAC) nên giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) vuông góc với (SAC)
Vậy giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Đúng 0
Bình luận (0)


