tính giá trị của biểu thức sau 2x8 -3y5 +2 tại x,y thõa mãn (x+1) 20 +(y+2)26 =0
DU
Những câu hỏi liên quan
1.Tính giá trị biểu thức: 6x^2+5x-2 tại x thõa mãn /x-2/=1
2.Tính giá trị biểu thức: 2x^8-3y^5+2 tại x,y thõa mãn (x+1)^20+(y+2)^26=0
3.Tính giá trị biểu thức: P=6x^3-4x^2y-14y^2+21xy+9 tại x,y thõa mãn 2x^2+7y=0
Mình đang cần gấp lắm ạ, mong mọi người giúp, mình cảm ơn nhiều ạ
Tính giá trị biểu thức : C = 2x5 - 5y3 + 2015 với x,y thõa mãn : |x - 1| + (y+2)20 = 0
|x-1| +(y+2)^20=0
|x-1| \(\ge0\)
(y+2)^20 \(\ge\)0
=> |x-1| +(y+2)^20\(\ge\) 0
"=" xảy ra khi x=1 y=-2
Với x=1 y=-2 thay vào tính C
Đúng 0
Bình luận (0)
cho biểu thức :\(P=\left(\frac{8}{x^2-16}+\frac{1}{x+4}\right):\frac{1}{x^2-2x-8}\)
1.Rút gọn biểu thức P
2.Tính giá trị của biểu thức P tại X thõa mãn \(x^2-9x+20=0\)
\(P=\left(\frac{8}{\left(x+4\right)\left(x-4\right)}+\frac{1}{x+4}\right):\frac{1}{x^2-2x-8}\)
\(P=\left(\frac{8}{\left(x+4\right)\left(x-4\right)}+\frac{x-4}{\left(x-4\right)\left(x+4\right)}\right)\cdot\frac{x^2-2x-8}{1}\)
\(P=\left(\frac{x+4}{\left(x+4\right)\left(x-4\right)}\right)\cdot x^2-2x-8\)
\(P=\frac{1}{x-4}\cdot x^2-2x-8\)
P\(P=\frac{x^2+2x-4x+8}{x-4}\)
\(P=\frac{x\left(x+2\right)-4\left(x+2\right)}{x-4}\)
\(P=\frac{\left(x-4\right)\left(x+2\right)}{x-4}\)
\(P=x+2\)
Đúng 0
Bình luận (0)
2 ,\(x^2-9x+20=0\)
\(\Rightarrow x^2-4x-5x+20=0\)
\(\Rightarrow x\left(x-4\right)-5\left(x-4\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-5=0\\x-4=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=5\\x=4\end{cases}}\)
\(\orbr{\begin{cases}x=5\Rightarrow\\x=4\Rightarrow\end{cases}}\orbr{\begin{cases}P=7\\P=6\end{cases}}\)
Đúng 0
Bình luận (0)
cho các số x,y thõa mãn đẳng thức \(x^2+xy+y^2+x-y+1=0\)
tính giá trị của biểu thức M=\(\left(x+y\right)^{30}+\left(x+2\right)^{12}+\left(y-1\right)^{2017}\)
ta có \(2x^2+2xy+2y^2+2x-2y+2=0\)
<=>\(x^2+2xy+y^2+x^2+2x+1+y^2-2y+1=0\)
<=>\(\left(x+y\right)^2+\left(x+1\right)^2+\left(y-1\right)^2=0\)
<=>\(\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
thay vào, ta có M=\(0^{30}+\left(-1+2\right)^{12}+\left(1-1\right)^{2017}=1\)
Vậy M=1
^_^
Đúng 0
Bình luận (0)
tính gia trị của biểu thức
2x8 -3x5+2 tại x,y thỏa mãn (x+1)20 +(y+2)26 =0
Vì \(\left(x+1\right)^{20}\ge0;\left(y+2\right)^{26}\ge0\) ( số mũ đều chẵn )
\(\Rightarrow\left(x+1\right)^{20}+\left(y+2\right)^{26}\ge0\)
Dấu "=" xảy ra <=> \(\left(x+1\right)^{20}=0;\left(y+2\right)^{26}=0\)
=> \(x+1=0;y+2=0\)
=> x = - 1; y = - 2
\(\Rightarrow2.x^8-3x^5+2=2.\left(-1\right)^8-3.\left(-1\right)^5+2=7\)
Đúng 0
Bình luận (0)
cho x, y là 2 số thực thõa mãn: x2 + 2y2 + 2xy + 7x +7y + 10 = 0
tìn giá trị nhỏ nhất và giá trị lớn nhất của biểu thức : A = x + y +1
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
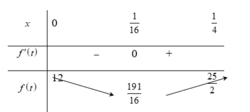
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
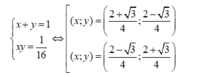
Chọn A.
Đúng 0
Bình luận (0)
Tính giá trị biểu thức C = 2x5 - 5y3 + 2015 tại x, y thỏa mãn |x - 1| + (y + 2)20 = 0
Ta có:
\(\left|x-1\right|+\left(y+2\right)^{20}=0\)
\(\Rightarrow\left|x-1\right|=0\) và \(\left(y+2\right)^{20}=0\)
+) \(\left|x-1\right|=0\Rightarrow x-1=0\Rightarrow x=1\)
+) \(\left(y+2\right)^{20}=0\Rightarrow y+2=0\Rightarrow y=-2\)
\(\Rightarrow C=2x^5-5y^3+2015\)
\(=2.1^5-5.\left(-2\right)^3+2015\)
\(=2-\left(-40\right)+2015\)
\(=2057\)
Vậy C = 2057
Đúng 1
Bình luận (1)
tính giá trị biểu thức A= x^2 - 2x + 2020 tại x thõa mãn \(|x-2|=0\)
Bài làm:
\(\left|x-2\right|=0\Rightarrow x=2\)
Khi đó: \(A=2^2-2.2+2020=2020\)
Tính x \(|x-2|=0\Rightarrow x=0+2=2\) ( Vì bằng 0 nên chỉ có 1 nghiệm )
Thay \(x=2\) vào \(A=x^2-2x+2020\) ta có :
\(A=2^2-2.2+2020=4-4+2020=2020\)
Vậy giá trị \(A=x^2-2x+2020\) với \(|x-2|=0\) là \(2020\)
\(\left|x-2\right|=0\Leftrightarrow x-2=0\Rightarrow x=2\)
Thay x = 2 vào A ta được :
\(A=2^2-2\cdot2+2020=4-4+2020=2020\)
Xem thêm câu trả lời




