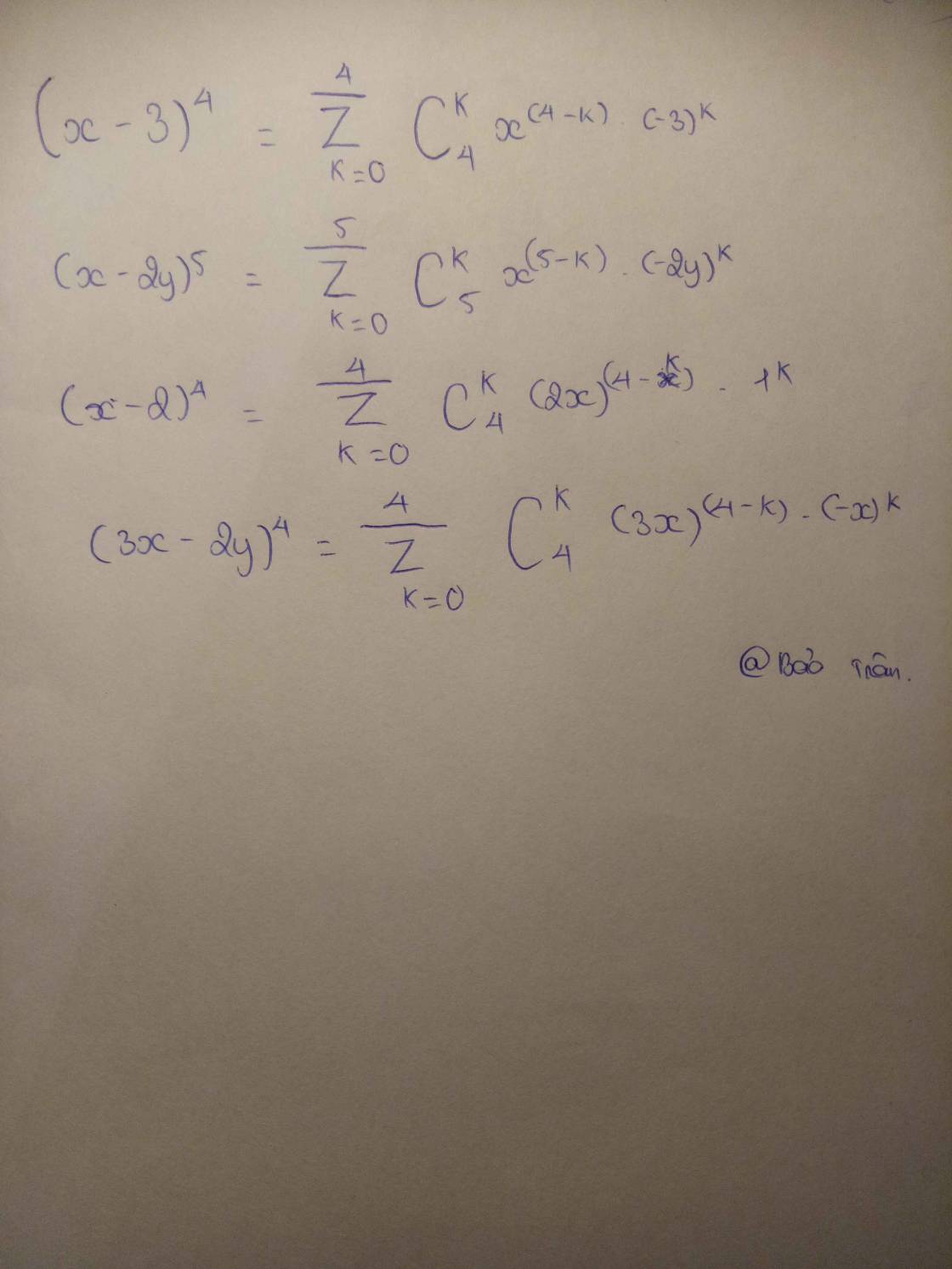khai triển (x+2y)^5 thành đa thức
MR
Những câu hỏi liên quan
khai triển (x+2y)^5 thành đa thức nếu được thì hãy giải rõ ràng ạ
x^5 + 5.x^4.2y + 10.x^3.4y^2 + 10.x^2.8y^3 + 5.x.16y^4 + 32y^5
= x^5 + 10.x^4.y + 40.x^3.y^2 + 80.x^2.y^3 + 80.x.y^4 +32.y^5
Đúng 2
Bình luận (0)
Tìm số hạng chứa
x
3
y
3
trong khai triển
(
x
+
2
y
)
6
thành đa thức A.
160
x
3
y
3
B.
20
x
3
y
3
C.
8...
Đọc tiếp
Tìm số hạng chứa x 3 y 3 trong khai triển ( x + 2 y ) 6 thành đa thức
A. 160 x 3 y 3
B. 20 x 3 y 3
C. 8 x 3 y 3
D. 120 x 3 y 3
khai triển các đa thức sau bằng nhị thức Newton
(x-3)^4 , (x-2y)^5 , (2x+1)^4 , (x-2)^4 , (3x-2y)^4
1. Khai triển biểu thức (x - 2y)3ta được kết quả là:
2. phân tích đa thức 8x3 -1 thành nhân tử
3. phân tích đa thức x2-2x - 4 y2+ 1 thành nhân tử
4. Cho hình bình hành ABCD có góc A = 60o. Khi đó, hệ thức nào sau đây là không đúng? (Chỉ được chọn 1 đáp án)
A GócA= nửa gócB
B. GócC = 600
C. Số đo gócD = 60o
D. GócB = 2gócC
1.\(\left(x-2y\right)^3=x^3-6x^2y+12xy^2-8y^3\)
2.\(8x^3-1=\left(2x-1\right)\left(4x^2+2x+1\right)\)
3. \(x^2-2x-4y^2+1=\left(x-1\right)^2-\left(2y\right)^2=\left(x-2y-1\right)\left(x+2y-1\right)\)
4.C
Đúng 0
Bình luận (0)
Khai triển các đa thức:
a) \({(x - 3)^4};\)
b) \({(3x - 2y)^4};\)
c) \({(x + 5)^4} + {(x - 5)^4};\)
d) \({(x - 2y)^5}\)
a) \(\begin{array}{l}{(x - 3)^4} = {x^4} + 4{x^3}.( - 3) + 6{x^2}.{( - 3)^2} + 4x.{( - 3)^3} + {( - 3)^4}\\ = {x^4} - 12{x^3} + 54{x^2} - 108x + 81\end{array}\)
b) \({(3x - 2y)^4} = 81{x^4} - 216{x^3}y + 216{x^2}{y^2} - 96x{y^3} + 16{y^4}\)
c)
\(\begin{array}{l}{(x + 5)^4} + {(x - 5)^4} = {x^4} + 20{x^3} + 150{x^2} + 500x + 625\\ + {x^4} - 20{x^3} + 150{x^2} - 500x + 625\\ = 2{x^4} + 300{x^2} + 1250\end{array}\)
d) \({(x - 2y)^5} = {x^5} - 10{x^4}y + 40{x^3}{y^2} - 80{x^2}{y^3} + 80x{y^4} - 32{y^5}\)
Đúng 0
Bình luận (0)
Cho Khai triển P(x) thành đa thức ta được Tính A.
S
-
20
.
5
19
B.
S
20
.
5
21
C.
S...
Đọc tiếp
Cho ![]() Khai triển P(x) thành đa thức ta được
Khai triển P(x) thành đa thức ta được ![]() Tính
Tính ![]()
A. S = - 20 . 5 19
B. S = 20 . 5 21
C. S = 20 . 5 19
D. S = 20 . 5 20
Đáp án D
Phương pháp:
Công thức nhị thức Newton ![]()
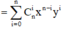
Cách giải:
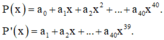
Ta có ![]()
![]()
![]()
![]()
Cho x =1
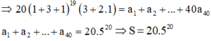
Đúng 0
Bình luận (0)
Tìm số hạng chứa
x
3
y
3
trong khai triển biểu thức
x
+
2
y
6
thành đa thức. A.
160
x
3
y
3
B.
120
x
3
y...
Đọc tiếp
Tìm số hạng chứa x 3 y 3 trong khai triển biểu thức x + 2 y 6 thành đa thức.
A. 160 x 3 y 3
B. 120 x 3 y 3
C. 20 x 3 y 3
D. 8 x 3 y 3
Đáp án A
Ta có: x + 2 y 6 = ∑ k = 0 6 C 6 k x 6 − k 2 y k = ∑ k = 0 6 C 6 k 2 k x 6 − k y k .
Số hạng chứa x 3 y 3 ⇒ 6 − k = 3 k = 3 ⇒ k = 3 ⇒ a 3 = C 6 3 2 3 x 3 y 3 = 160 x 3 y 3 .
Đúng 0
Bình luận (0)
Tìm số hạng chứa
x
3
y
3
trong khai triển biểu thức
x
+
2
y
6
thành đa thức. A.
160
x
3
y
3
B.
120
x...
Đọc tiếp
Tìm số hạng chứa x 3 y 3 trong khai triển biểu thức x + 2 y 6 thành đa thức.
A. 160 x 3 y 3
B. 120 x 3 y 3
C. 20 x 3 y 3
D. 8 x 3 y 3
khai triển thành hằng đẳng thức: x^2+y^2+2x+2y+2(x+1)(y+1)+2
Xem chi tiết
\(x^2+y^2+2x+2y+2\left(x+1\right)\left(y+1\right)+2\)
\(=x^2+2x+1+y^2+2y+1+2\left(x+1\right)\left(y+1\right)\)
\(=\left(x+1\right)^2+2\left(x+1\right)\left(y+1\right)+\left(y+1\right)^2\)
\(=\left(x+1+y+1\right)^2\)
\(=\left(x+y+2\right)^2\)