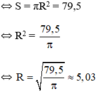tính S hình tròn biết bán kính r
r = 68
DD
Những câu hỏi liên quan
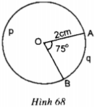
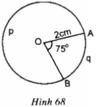
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính diện tích hình quạt tròn OAqB
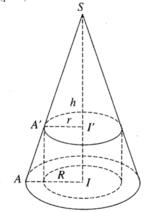
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h. Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H). Tính tỉ số thể tích của (H') và (H)
Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.
Khi đó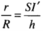 
Do đó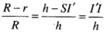 
Từ đó suy ra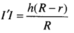 
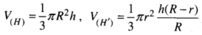
Do đó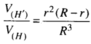 
Đúng 0
Bình luận (0)
Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính sđ A p B ⏜
Biết bán kính của hình tròn là một số nguyên ( r ) Tính chu vi (P) và diện tích (S) của hình tròn.
program bai_giai;
uses crt;
var r,P,S:real;
begin
clrscr;
write('Nhap ban kinh: '); readln(r);
P:=2*r*3.14;
S:=r*r*3.14;
writeln('Chu vi P la: ',p:0:2);
writeln('Dien tich S la: ',s:0:2);
readln;
end.
Đúng 1
Bình luận (0)
Dùng máy tính cầm để:a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2b) Công thức tính diện tích S của hình tròn bán kính R là S pi {R^2}. Tính bán kính của một hình tròn có diện tích là 100 cm2.
Đọc tiếp
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
a) Độ dài cạnh của một mảnh đất hình vuông là:
\(\sqrt {12\,\,996} = 114\)(m)
b) Bán kính của hình tròn là:
\(S = \pi {R^2} \Rightarrow R^2 = \frac{S}{\pi } \Rightarrow R = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{100}}{\pi }} \approx 5,64\)(cm)
Đúng 0
Bình luận (0)
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính độ dài hai cung AqB và ApB
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h. Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H). Xác định r để (H') có thể tích lớn nhất.
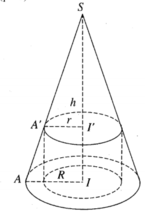
V H ' lớn nhất khi f(r) = r 2 (R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3 r 2 = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
Khi đó 
Đúng 0
Bình luận (0)
Diện tích S của hình tròn được tính bởi công thức
S
π
R
2
, trong đó R là bán kính của hình tròn.a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
R (cm)
0,57
1,37
2,15
4,09
S πR2
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)b) Nếu bán kính tăng gấp 3 lần...
Đọc tiếp
Diện tích S của hình tròn được tính bởi công thức S = π R 2 , trong đó R là bán kính của hình tròn.
a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 |
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)
b) Nếu bán kính tăng gấp 3 lần thì diện tích tăng hay giảm bao nhiêu lần?
c) Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.
a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:
Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
Đúng 0
Bình luận (0)