Trong mặt phẳng tọa độ lấy các điểm A(0;6), B(6;0) và C(1;1)
Tính diện tích tam giác ABC
Trong không gian với hệ tọa độ Oxyz lấy các điểm A(a;0;0), B(0;b;0), C(0;0;c) trong đó a > 0 , b > 0 , c > 0 và 1 a + 1 b + 1 c = 2 . Khi a, b, c thay đổi, mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ
A. (1;1;1)
B. (2;2;2)
C. 1 2 ; 1 2 ; 1 2
D. - 1 2 ; - 1 2 ; - 1 2
Phương trình mặt chắn của mặt phẳng (ABC) là: ![]()
Từ giả thiết 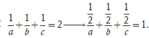 Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
A. 6 x − 3 y − 2 z − 12 = 0
B. 6 x + 3 y + 2 z − 12 = 0
C. 6 x − 3 y − 2 z + 12 = 0
D. 6 x − 3 y + 2 z − 12 = 0
Đáp án A.
6 x - 3 y + 2 z - 12 = 0 .
Tương tự
B 0 ; 4 ; 0 , C 0 ; 0 ; 6 ⇒ A B C : x 2 + y 4 + z 6 = 1 ⇔ 6 x + 3 y + 2 z − 12 = 0.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A.M( 4; 0)
B.M( 0; 4)
C.M( 5;3)
D.M( 2; 8)
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A. M(4; 0)
B. M(0; 4)
C. M(5;3)
D. M(2; 8)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
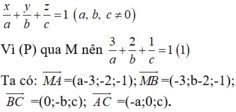
Vì M là trực tâm của tam giác ABC nên:
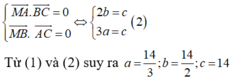
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
trong mặt phẳng tọa độ tìn vị trí các điểm có tọa độ x;y thảo mãn 1 trong các điều kiện
a) Điểm A : x(y-1)=0
b ) Điểm B : (x+y)(y-2)=0
c ) Điểm C : (x-1)^2+(y+2)^2=0
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A . P : 2 x - y + 3 z = 0
B . P : 6 x - 3 y + 5 z = 0
C . P : 2 x - y - 3 z = 0
D . P : - 6 x + 3 y + 4 z = 0