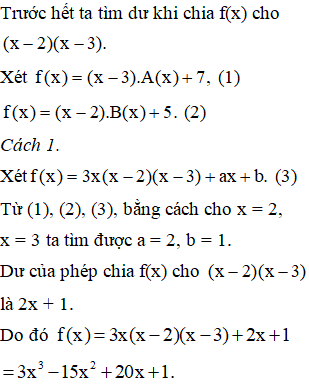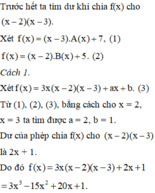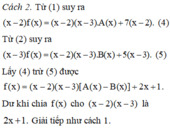tìm đa thức f(x) . Biết f(x) chia cho (2x^2+3x+1) được thương là x+7 và còn dư; khi chia f(x) cho x-5 dư 745 và f(x) cho x-1 dư 41
NL
Những câu hỏi liên quan
Tìm đa thức f(x) sao cho f(x) chia cho x - 2 dư 1 , f(x) chia cho x + 5 dư 8 , f(x) chia cho x^2 + 3x - 10 được thương là 2x và còn dư .
GỌI THƯƠNG CỦA PHÉP CHIA f(x) cho (x-2) và (x+5) lần lượt là p(x) và Q(x)
theo bài ra ta có
\(\hept{\begin{cases}f._x=\left(x-2\right).p._{\left(x\right)}+1............\left(1\right)\\f._{\left(x\right)}=\left(x+5\right).Q._{\left(x\right)}+8.......\left(2\right)\end{cases}}\)
GỌI THƯƠNG CỦA PHÉP CHIA f(x) cho (x-2)(x+5) [ là x^2+3x-10 phân tích thành] =2x là g(x) và số dư là nhị thức bậc nhất là ax+b
ta có, \(f._{\left(x\right)}=\left(x-2\right)\left(x+5\right).g._{\left(x\right)}+ax+b....................\left(3\right)\)
TỪ (1) VÀ (3) TA CÓ X=2 THÌ \(\hept{\begin{cases}f._2=1\\f_2=2a+b\end{cases}}\)
=> 2a+b=1 =>b=1-2a (4)
TỪ (2) VÀ (3) TA CÓ X=-5 THÌ \(\hept{\begin{cases}f_{\left(-5\right)}=8\\f_{\left(-5\right)}=-5a+b\end{cases}}\)
=> 8=-5a+b =>b=8+5a (5)
TỪ (4) VÀ (5) =>1-2a=8+5a <=> a=-1
=> b=3
vậy số dư là -x+3
vậy đa thức f(x) =(x-2)(x+5) .2x+(-x+3)=\(2x^3+6x^2-21x+3\)
Đúng 0
Bình luận (0)
tìm đa thức f(x), biết f(x)chia x-3 dư 7,chia cho x-2 dư 5, chia (x-2)(x-3)thì được thương là 3x và còn dư
Vì f(x) chia x-3 dư 7
\(\Rightarrow f\left(x\right)=\left(x-3\right)q\left(x\right)+7\)
\(\Rightarrow f\left(3\right)=7\)
Vì f(x) chia x-2 dư 5
\(\Rightarrow f\left(x\right)=\left(x-2\right)q\left(x\right)+5\)
\(\Rightarrow f\left(2\right)=5\)
Ta có f(x) khi chia (x-2)(x-3) thì được thương là 3x và còn dư
\(\Rightarrow f\left(x\right)=\left(x-2\right)\left(x-3\right)3x+ax+b\)
\(\Rightarrow\hept{\begin{cases}f\left(2\right)=2a+b=5\\f\left(3\right)=3a+b=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=2\\b=1\end{cases}}\)
Vậy \(f\left(x\right)=\left(x-2\right)\left(x-3\right)3x+2x+1\)
tìm đa thức f(x) ,biết rằng f(x) chia x-3 dư 7,f(x) chia x-2 dư 5,chia (x-2)(x-3) thì được thương là 3x và còn dư
rfyfhjd fdued rdf fdu fusb 34 hfuc * 45 jd bj gdjfjeitbig hkffr giodsd fdfb
tìm đa thức f(x) biết rằng f(x) chia cho x-3 dư 7 f(x) chia cho x-2 dư 5 f(x) chia cho (x-2)(x-3) thì thương là 3x và còn dư
Xem thêm câu trả lời
A: TÌm đa thức f(x) biết f(x) chia x+2 dư 10, f(x) chia x-2 dư 24, chia cho x^2-4 được thương là -5x và còn dư
B: TÌm các số nguyên x,y thỏa mãn:
X^3+2x^2+3x+2=y^3
Tìm đa thức f(x) biết rằng f(x) chia cho x+3 thì dư 1, chia cho x-4 thì dư 8, chia cho (x+3)(x-4) thì được thương là 3x và còn dư
F(x) = ( x + 3 )( x - 4 ).3x + ax + b
F(-3) = 1 => -3a + b = 1 => b = 1 + 3a
F(4) = 8 => 4a + b = 8 thay b = 1 + 3a
=> 7a + 1 = 8 => a = 1 => b = 1 + 3 = 4
=> f(x) = ( x + 3 )( x - 4 ).3x + x + 4
đến đây chỉ việc nhân ra thôi
Đúng 0
Bình luận (0)
Tìm đa thức F(x) biết F(x) chia x+2 dư 8, F(x) chia x-5 dư 26, F(x) chia \(\left(x+2\right)\left(x+5\right)\) được thương là 2x và còn dư
Chia $(x+2)(x+5)$ hay $(x+2)(x-5)$ vậy bạn?
Đúng 0
Bình luận (1)
Tìm đa thức F(x) biết F(x) chia x+2 dư 8, F(x) chia x-5 dư 26, F(x) chia \(\left(x+2\right)\left(x-5\right)\) được thương là 2x và còn dư
Lời giải:
Gọi $ax+b$ là dư của $F(x)$ khi chia cho $(x+2)(x-5)$
Ta có:
$F(x)=2x(x+2)(x-5)+ax+b(*)$
Theo đề thì $F(-2)=8; F(5)=26$
Thay $x=-2$ vào $(*)$ thì:
$F(-2)=(-2)a+b=8(1)$
$F(5)=5a+b=26(2)$
Từ $(1); (2)\Rightarrow a=\frac{18}{7}; b=\frac{92}{7}$
Khi đó:
$F(x)=2x(x+2)(x-5)+\frac{18}{7}x+\frac{92}{7}$
$=2x^3-6x^2-\frac{122x}{7}+\frac{92}{7}$
Đúng 1
Bình luận (0)
a) Cho đa thức f(x) = x^100 + x^99 + ... + x^2 + x + 1 . tìm dư của phép chia đa thức f(x) cho đa thức x^2 -1
b) Tìm đa thức f(x) biết rằng f(x) chia cho x-2 thì dư 2, f(x) chia cho x-3 thì dư 7 , f(x) chia cho x^5 - 5x + 6 thì đc thương là 1 - x^2 và còn dư
Huyền hỏi 2 bài liên tiếp à viết nhanh thế
Đúng 1
Bình luận (0)
Các dạng bài này đc giải rất nhiều sao bạn ko coi thế?
Đúng 1
Bình luận (0)