mọi người làm giúp tui bài này mới:
CM:210+512 là hợp số!
bài này làm thế nào mọi người giúp tui với
Mọi người dịch giúp tui câu này:
Bạn đang làm gì vậy?Mình đang học bài.
Dịch giúp mình nha
What are you doing? I'm studing
Ko có gì
Ok, mình kb đây
Mọi người giúp tui hai bài này với tui cảm ơn nhiều :)) 
Trong tập hợp số tự nhiên, hãy tìm một dãy 2000 số tự nhiên liên tiếp mà không có 1 số nguyên tố nào
Mọi người ơi làm ơn giúp mình làm bài này với. Xin mọi người giúp đỡ
Do dãy 2000 số tự nhiên liên tiếp đó không có số nguyên tố nào nên chúng là hợp số.
Coi dãy đó chứa các số tự nhiên liên tiếp từ a + 2 đến a + 2001 \(\left(a\in N\right)\)
Để tất cả các số trên là hợp số thì a phải chia hết các số từ 2 đến 2001, vì vậy a = 2001!
Thế vào các số trên, ta có:
- a + 2 = 2001! + 2 = 2 ( 3 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 3 = 2001! + 3 = 3 ( 2 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 4 = 2001! + 4 = 4 ( 2 * 3 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
...................................................................................................................................
- a + 2001 = 2001! + 2001 = 2001 ( 2 * 3 * 4 * ... * 2000 + 1 ) ( là hợp số ) - thoả mãn
Vậy trong tập hợp số tự nhiên, dãy có 2000 số tự nhiên liên tiếp mà không có 1 số nguyên tố nào là:
2001! + 2 ; 2001! + 3 ; 2001! + 4 ; .... ; 2001! + 1999 ; 2001! + 2000 ; 2001! + 2001
Giúp tui giải bài này với mọi người ! Tui cần gấp lắm !
bài nào vậy bạn
Hình ảnh nó chưa kịp chạy đó bạn mình có đăng lại câu hỏi òi
-Nhờ mọi người làm giúp tui bài này với. Ngày mai tui nộp rồi.
Cho a,b,c là ba số thực dương. Chứng minh rằng:
\(\dfrac{3}{2}\le\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\le\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\)
a/(b+c) + b/(a+c) + c/(a+b) = a^2/(ab+ac) + b^2/(ba+bc) + c^2/(ac+bc) >=
(a+b+c)^2/(2.(ab+bc+ac) (buhihacopxki dạng phân thức)
>= (3.(ab+bc+ac)/(2(ab+bc+ac) =3/2
a^2/(b^2+c^2) + b^2/(a^2+c^2) + c^2/(a^2+b^2) >= (a+b+c)^2/(2.(a^2+b^2+c^2) (buhihacopxki dạng phân thức)
>= 3(a^2+b^2+c^2) / 2(a^2+b^2+c^2) >=3/2
\(\Leftrightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}-\dfrac{3}{2}\ge0\)
\(\Leftrightarrow\left(\dfrac{a}{b+c}-\dfrac{1}{2}\right)+\left(\dfrac{b}{c+a}-\dfrac{1}{2}\right)+\left(\dfrac{c}{a+b}-\dfrac{1}{2}\right)\ge0\)
\(\Leftrightarrow\left(\dfrac{2a-b-c}{2\left(b+c\right)}\right)+\left(\dfrac{2b-a-c}{2\left(a+c\right)}\right)+\left(\dfrac{2c-a-b}{2\left(a+b\right)}\right)\ge0\)
\(\Leftrightarrow\dfrac{a-b+a-c}{2\left(b+c\right)}+\dfrac{b-a+b-c}{2\left(a+c\right)}+\dfrac{c-a+c-b}{2\left(a+b\right)}\ge0\)
\(\Leftrightarrow\dfrac{a-b}{2\left(b+c\right)}+\dfrac{a-c}{2\left(b+c\right)}+\dfrac{b-a}{2\left(a+c\right)}+\dfrac{b-c}{2\left(a+c\right)}+\dfrac{c-a}{2\left(a+b\right)}+\dfrac{c-b}{2\left(a+b\right)}\ge0\)\(\Leftrightarrow\left(a-b\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+c\right)}\right]+\left(a-c\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]+\left(b-c\right)\left[\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\)
ta có: a,b,c là 3 số dương bất kì nên ta giả sử \(a\ge b\ge c\)
\(\Rightarrow a+c\ge b+c\)
\(\Leftrightarrow2\left(a+c\right)\ge2\left(b+c\right)\)
\(\Leftrightarrow\dfrac{1}{2\left(a+c\right)}\le\dfrac{1}{2\left(b+c\right)}\)
\(\Leftrightarrow\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(b+c\right)}\ge0\)
Mà \(a\ge b\Rightarrow a-b\ge0\)
\(\Rightarrow\left(a-b\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+c\right)}\right]\ge0\left(1\right)\)
Chứng minh tương tự, ta có:
\(\left(a-c\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\left(2\right)\)
\(\left(b-c\right)\left[\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\left(3\right)\)
Cộng từng vế (1);(2);(3) \(\Rightarrow\) luôn đúng
\(\Rightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge\dfrac{3}{2}\)
Một phép chia có thương là 4 số dư bằng 25. Tổng của số bị chia, số chia và số dư bằng 210. Tìm số bị chia và số chia
Mọi người giúp em bài toán này nhé "đc like"
Theo đề bài ta có:a:b=4(dư 25)
a+b=210
Thay a=4b+5 vào (1) ta được:
4b+25+b+25=210
5b+50=210
5b=210-50
5b=160
b=160:5
b=32
Thay b=32 vào (2) ta được:
a=32x4+25
a=128+25
a=153
Gọi a là số bị chia,b là số chia.
Theo đèbài,ta có:
a:b=4(dư 25)
a+b=210
Ta được:
a+25+b+25=210
a+b+50 =210
a+b =210-50
a+b = 160
Vậy 160 là tổng của a;b.
Số bị chia a gấp 4 lần số chia b.
Ta có thể nói số chia b=1/4 số bị chia a.
Giá trị 1 phần cũng là số chia:
160:(4+1)=32
Số bị chia:
160-32+25=153
Đ/S:SBC:153
SC :32
mọi người giúp mik làm bài này nha
Ba đơn vị kinh doanh cùng góp vốn làm ăn chung . Biết số vốn của đơn vị là 1 và 2 tỉ lệ với 2 và 3 . Biết số vốn của đơn vị 1 và 2 tỉ lệ với 4 và 5 . Cuối năm chia lãi số tiền 210 triệu . Hỏi số tiền lãi của mỗi đơn vị biết số tiền lãi tỉ lệ với số vốn đóng góp
bài toán trên là bài toán về tỉ lệ thuận nha ! Ai làm được đúng và nhanh nhất mik sẽ tick cho người đó ^_^
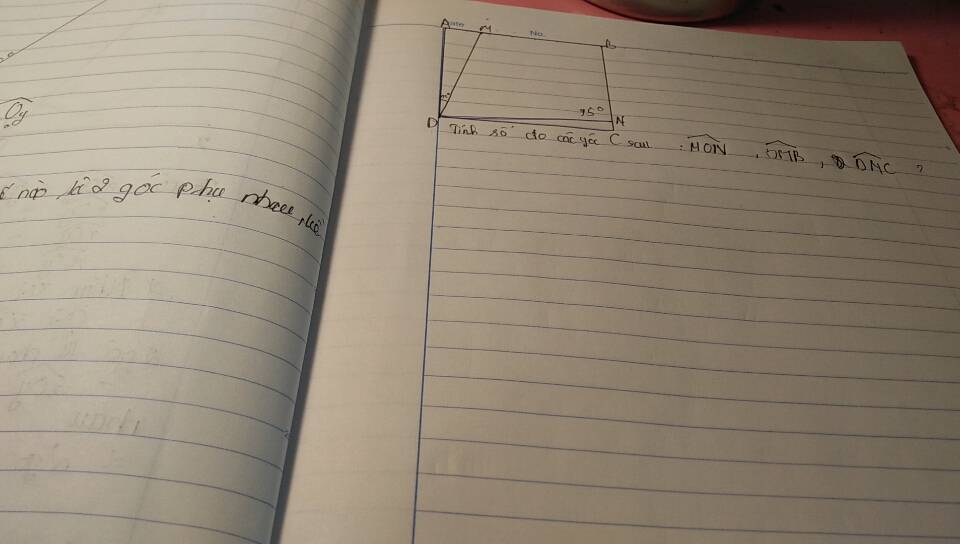
mọi người ơi cứu em bài này với, cô bảo là làm hình này trong logo mọi người giúp em với ;-;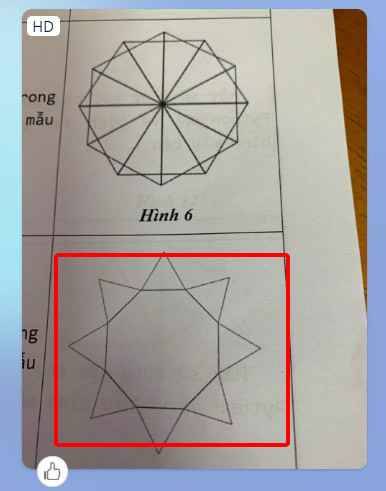
repeat 8[repeat 3[fd 100 rt 120]fd 100 lt 360/8]