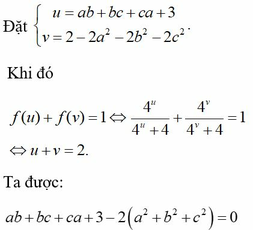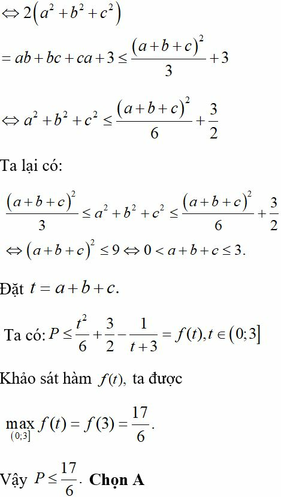tìm các số nguyên tố a,b nhỏ nhất sao cho a2-2b2=1
LV
Những câu hỏi liên quan
Biết rằng tồn tại các số nguyên a, b sao cho hàm số
y
a
x
+
b
x
2
+
1
đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của
a
2
+
2
b...
Đọc tiếp
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
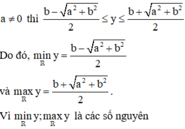
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
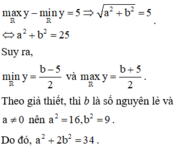
Đúng 0
Bình luận (0)
cho a,b là các số nguyên dương thỏa mãn a2-ab+3/2b2 chia hết cho 25. Chứng minh rằng cả a và b đều chia hết cho 5.
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Đọc tiếp
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
cho p là số nguyên tố lớn hơn 3. chứng minh p2 -1 chia hết cho 24
tìm số tự nhiên n sao cho n+1, n+77, n+99 đều là các số nguyên tố
cho a+b=c+d=e+f với a,b,c,d,e,f là các số nguyên tố phân biệt, nhỏ hơn 20. Tìm a+b
tìm số nguyên tố p sao cho p+2, p+94 là các số nguyên tố
Cho số Nguyên tố a;b;c ; cho các stn m khác 0 . sao cho a2+b2+25c2=9m2+1
1.Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 7,cho 13,cho 17có số dư lần lượt là 3,11,14.2.Tìm 2 số tự nhiên a và b (ab) biết BCNN (a,b) + ƯCLN (a,b) 193.Tìm tất cả những cặp số tự nhiên (x;y) sao cho 6x +9920y4.Tổng của 38 số tự nhiên lẻ liên tiếp bằng 2052.Tìm số nhỏ nhất.5.Cho A4 + 42 + ................489Tìm số dư khi chia A cho 856.1xy là bội của 9 và là số nguyên tố nhỏ nhất .Tìm x,y7.Tìm số nguyên tố P sao cho các số sau cũng là số nguyên tố : P+2 và P+10GIÚP MÌNH VỚI , BIẾT LÀM...
Đọc tiếp
1.Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 7,cho 13,cho 17có số dư lần lượt là 3,11,14.
2.Tìm 2 số tự nhiên a và b (a<b) biết BCNN (a,b) + ƯCLN (a,b) = 19
3.Tìm tất cả những cặp số tự nhiên (x;y) sao cho 6x +99=20y
4.Tổng của 38 số tự nhiên lẻ liên tiếp bằng 2052.Tìm số nhỏ nhất.
5.Cho A=4 + 42 + ................489
Tìm số dư khi chia A cho 85
6.1xy là bội của 9 và là số nguyên tố nhỏ nhất .Tìm x,y
7.Tìm số nguyên tố P sao cho các số sau cũng là số nguyên tố : P+2 và P+10
GIÚP MÌNH VỚI , BIẾT LÀM BÀI NÀO THÌ CỨ LÀM ,KHÔNG BIẾT THÌ KHÔNG SAO
AI NHANH NHẤT VÀ ĐÚNG NHẤT MÌNH TICK CHO 2 TICK ! ! ! ! !
1. Ta có: a chia có 7 dư 3 => a - 3 chia hết cho 7
=> 4 (a - 3) chia hết cho 7 => 4a - 12 chia hết cho 7
=> 4a - 12 + 7 chia hết cho 7 => 4a - 5 chia hết cho 7 (1)
a chia cho 13 dư 11 => a - 11 chia hết cho 13
=> 4 (a - 11) chia hết cho 13 => 4a - 44 chia hết cho 13
=> 4a - 44 + 39 chia hết cho 13 => 4a - 5 chia hết cho 13 (2)
a chia cho 17 dư 14 => a - 14 chia hết cho 17
=> 4 ( a - 14) chia hết cho 17 => 4a - 56 chia hết cho 17
=> 4a - 56 + 51 chia hết cho 17 => 4a - 5 chia hết cho 17 (3)
Từ (1), (2) và (3) => 4a - 5 thuộc BC(7;13;17)
Mà a nhỏ nhất => 4a - 5 nhỏ nhất
=> 4a - 5 = BCNN(7;13;17) = 7 . 13 . 17 = 1547
=> 4a = 1552 => a= 388
2. Gọi ƯCLN(a,b) = d
=> a = d . m (ƯCLN(m,n) = 1)
b = d . n
Do a < b => m<n
Vì BCNN(a,b) . ƯCLN(a,b) = a . b
\(\Rightarrow BCNN\left(a,b\right)=\frac{a\cdot b}{ƯCLN\left(a,b\right)}=\frac{d\cdot m\cdot d\cdot n}{d}=m\cdot n\cdot d\)
Vì BCNN(a,b) + ƯCLN(a,b) = 19
=> m . n . d + d = 19
=> d . (m . n + 1) = 19
=> m . n + 1 thuộc Ư(19); \(m\cdot n+1\ge2\)
Ta có bảng sau:
Vậy (a,b) = (2;9) ; (1 ; 18)
3.
a)tìm b nhỏ nhất biết b:7 dư 2 b:6 dư 5
b)tìm 1 số tự nhiên a nhỏ nhất biết a: 12,15,16 đều dư 3
c)tìm số nguyên tố p sao cho p+20 và p+26 đều là số nguyên tố
Cho dãy số chứa trong list a0,a1,a2,..... Gọi M là tích các số trong list từ a0*a1*a2.... . Hãy tìm số nguyên dương d nhỏ nhất sao cho d không phải là ước số của M
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4