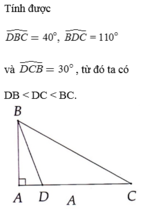
cho tam giác ABC đều, D thuộc AB. So sánh các cạnh của tam giác BDC
ND
Những câu hỏi liên quan
Cho tam giác ABC đều, điểm D thuộc cạnh AB. So sánh độ dài các cạnh của tam giác BDC.
Cho tam giác ABC có A ^ = 90 ° , B ^ = 30 ° . Điểm D thuộc cạnh AC sao cho A B D ^ = 20 ° . So sánh các độ dài các cạnh của tam giác BDC.
cho tam giác đều abc, điểm d thuộc cạnh ab. So sánh độ dài các cạnh tam giác BCD
Cho tam giác ABC có góc A =90°,góc C =30°.Điểm D thuộc cạnh AC sao cho góc ABD=20°.So sánh các độ dài các cạnh của tam giác BDC
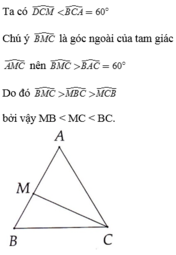
Cho tam giác đều ABC, điểm M thuộc cạnh AB. So sánh độ dài các cạnh của tam giác BMC.
2, cho tam giác abc vuông ở a có góc b=60 độ. kẻ tpg góc b cắt ac tại d.
a.tính góc adb và góc bdc
b.so sánh các cạnh của tam giác abd
c. so sánh các góc của tam giác bdc
a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
Góc BAC = 90 độ (do tam giác ABC vuông tại A) Góc B = 60 độ (theo đề bài) Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ) Góc ABD = Góc ABC (do AB // CD theo định lý Thales) Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30 Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC) Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 = AC^2 + BC^2 = a^2 + b^2 BC = a AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.
Đúng 0
Bình luận (0)
a. Tính góc ADB và góc BDC: Gọi góc ADB = x, góc BDC = y. Ta có thể sử dụng các quy tắc góc chắn cung và góc nội tiếp để tính góc như sau:
Góc BAC = 90 độ (do tam giác ABC vuông tại A) Góc B = 60 độ (theo đề bài) Góc ABC = 180 - Góc BAC - Góc B = 30 độ (tổng các góc của tam giác ABC bằng 180 độ) Góc ABD = Góc ABC (do AB // CD theo định lý Thales) Góc DAB = 180 - Góc ADB - Góc ABD = 180 - x - 30 Góc BCD = Góc BAC (do CD là tiếp tuyến của đường tròn ngoại tiếp tam giác BDC) Góc BDC = 180 - Góc BCD - Góc B = 90 - Góc BAC/2 = 45 độ (do tam giác BCD cân tại B)b. So sánh các cạnh của tam giác ABD: Để so sánh các cạnh của tam giác ABD, ta cần tính độ dài các cạnh. Theo định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 = AC^2 + BC^2 = a^2 + b^2 BC = a AC = b Vậy AB = sqrt(a^2 + b^2). Tương tự, ta có CD = b và BD = c*sqrt(3)/2 (tính theo phương pháp trong câu trả lời trước). Do đó, ta có thể so sánh các cạnh của tam giác ABD theo thứ tự tăng dần: CD < AB < BD.c. So sánh các góc của tam giác BDC: Trong tam giác BDC, ta đã tính được góc BDC = 45 độ (như ở câu a). Do tam giác BDC cân tại B, nên góc CBD cũng bằng 45 độ. Vì vậy, hai góc của tam giác BDC bằng nhau và bằng 45 độ.
Đúng 0
Bình luận (0)
Cho tam giác ABC đều có cạnh bằng 1. Dựng ra bên ngoài tam giác ABC tam giác BDC cân tại D
và góc BDC = 120 độ. Gọi M, N là hai điểm thuộc cạnh AB, AC tương ứng sao cho góc MDN = 60 độ. Tính chu vi tam giác AMN.
Bài 3 : Cho tam giác ABC vuông tại A và góc B lớn hơn góc C . Vẽ phân giác góc B cắt cạnh AC tại D , vẽ DE song song với BC ( E thuộc cạnh AB ) a) Chứng minh rằng tam giác BDE là tam giác cân b) Vẽ phân giác góc BDC cắt BC tại F , so sánh hai độ dài DF và CF c) Khi cho thêm điều kiện 0 C = 30 , hãy c/m tam giác ABF đều
cho tam giác ABC vuông tại A, góc B lớn hơn góc C.Phân giác góc B cắt AC tại D, vẽ DE//BC(E thuộc AB)
a.chứng minh tam giác BDE cân
b.Phân giác của góc BDC cắt BC tại F, so sánh DF và CF
c.khi cho thêm điều kiện góc C=30 độ , cm tam giác ABF là tam giác đều