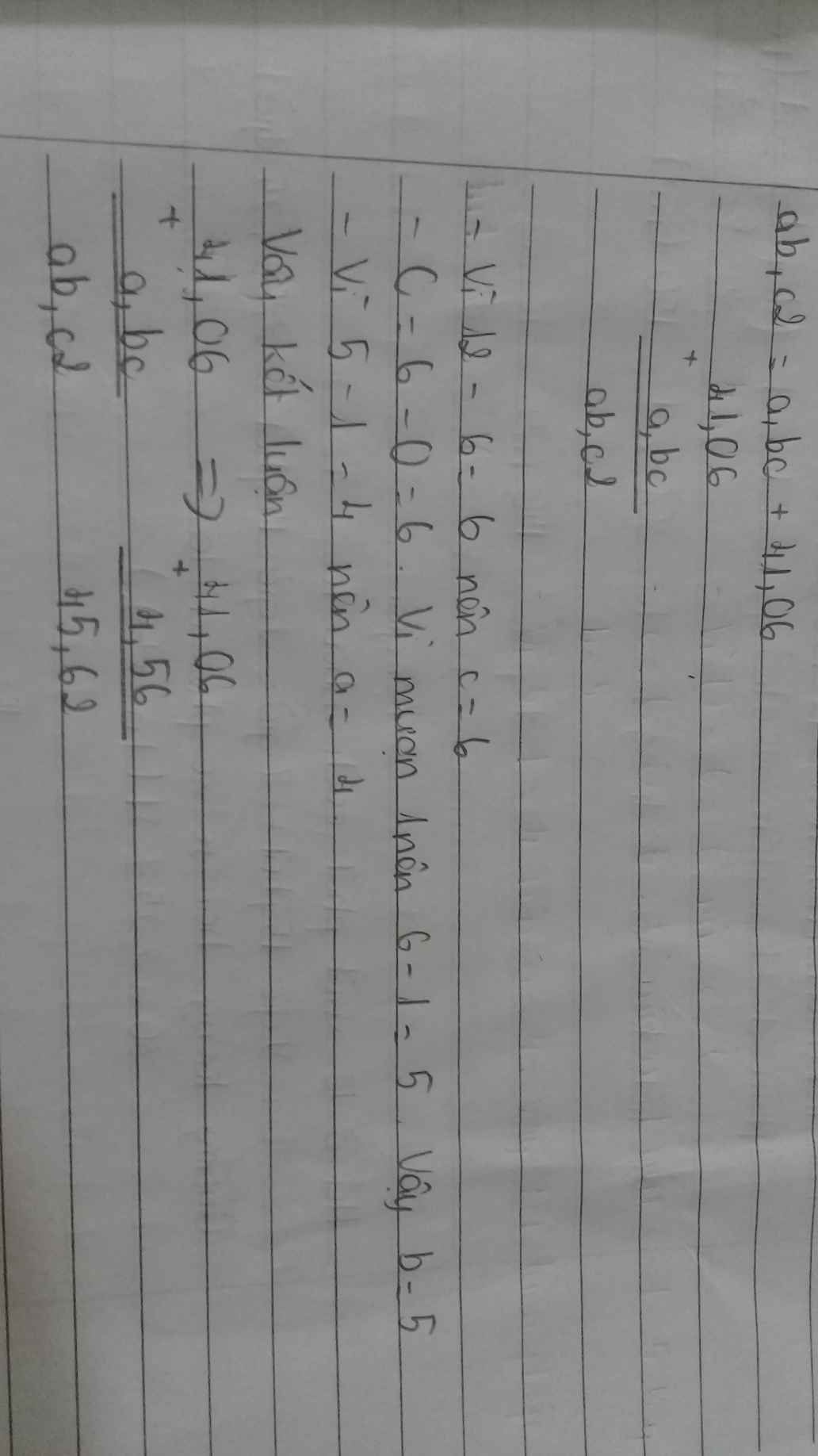tim ab biet: abc = ab +bc+ca
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Tim abc biet abc=ab+ac+ba+bc+ca+cb
a=3 b=9 c=6
=> 39+36+93+96+63+69
=>396
Đúng 0
Bình luận (0)
Tim stn a,b,c , biet abc < ab + bc + ca
Mik làm vậy các bn xem đúng ko nha
Vì abc < ab + bc + ca
<=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}>1\left(1\right)\)
Giả sử a > b > c => \(\frac{1}{a}< \frac{1}{b}< \frac{1}{c}\)
\(1< \frac{1}{a}+\frac{1}{b}+\frac{1}{c}< \frac{1}{c}+\frac{1}{c}+\frac{1}{c}=\frac{3}{c}\)=> c < 3 => c= 2
Thay c = 2 vào (1) ta được :
\(\frac{1}{2}< \frac{1}{a}+\frac{1}{b}< \frac{1}{b}+\frac{1}{b}=\frac{2}{b}=>2< b< 4=>b=3\)
thay b = 3 , c = 2 ta được
\(\frac{1}{a}>1-\frac{1}{2}-\frac{1}{3}=\frac{1}{6}=>a< 3< 6=>a=5\)
Vậy bộ số ( a ; b ;c ) = ( 2 ; 3 ; 5 )
Đúng 0
Bình luận (0)
Giả sử a = 2 ; b = 3 ; c = 5
=> a . b . c = 2 . 3 . 5 = 30
=> ab + bc + ca = ( 2.3 ) + ( 3 . 5 ) + ( 2 . 5 )
=> ab + bc + ca = 6 + 15 + 10
=> ab + bc + ca = 31
Mak 30 \(\ne\)31
=> Bn nguyễn thị thanh thảo làm sài!
Đúng 0
Bình luận (0)
mình giải thích \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}>1\)vì \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{b}{ab}+\frac{a}{ab}+\frac{1}{c}=\frac{a+b}{ab}+\frac{1}{c}=\frac{c.\left(a+b\right)}{abc}+\frac{ab}{abc}=\frac{ac+bc+ab}{abc}\)Mà abc<ab+bc+ca=>\(\frac{ab+bc+ac}{abc}\)>1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tim abc biet abc=ab+ba+ca
abc=ab+ba+ca
100a+10b+c=10a+b+10b+c+10c+a
100a+10b+c=11a+11b+11c
Ta có 100a+10b+c-11a-10b-c=11a+11b+11c-10b-c-11a
89a=b+10c
89a=bc => a=1 vì nếu a>1 thì bc>99 (Vô lí)
=> cb=89
Vậy abc=198
Đúng 0
Bình luận (0)
Đào Đức Mạnh bạn í viết sai đề mà bạn làm hay thế ^^, copy quên ko đối chiếu ak
Đúng 0
Bình luận (0)
28
tim so abc biet abc=ab+ba+bc+cb+ca+ac;voiabc la ba so tu nhien khac nhauva khac 0, biet a la so chan
100a+10b+c=10a+b+10b+a+10b+c+10c+b+10c+a+10a+c
=>100a+10b+c=22a+22b+22c
=>78a=12b+21c
=>26a=4b+7c
Đúng 0
Bình luận (0)
tim a,b,c biet a+b+c+ab+bc+ca chia het cho abc
ai lam nhanh trong 10 phut minh tang 9 tick
tim abc biet abc +ab,c+a,bc
tim a;b;c biet
ab=c bc=4a ca=9b
ab=c => a=c/b (1)
bc=4a => a=(bc)/4 (2)
Từ (1) và (2) => c/b = (bc)/4
<=> 1/b = b/4 <=> b^2 =4 <=> b = 2 hoặc b = -2
(*) Với b=2 thì
(1) => a=c/2 <=> c=2a
ta có: ac=9b nên 2a^2 = 18 <=> a^2 = 9 <=> a=3 hoặc a=-3
_ với a=3 thì c= 2*3 = 6 (thỏa)
_với a=-3 thì c= 2*-3 =-6 (thỏa)
(*) Với b=-2 thì
(1) => a=c/-2 <=> c=-2a
ta có: ac=9b nên -2a^2 = -18 <=> a^2 = 9 <=> a=3 hoặc a=-3
_ với a=3 thì c= -2*3 = -6 (thỏa)
_với a=-3 thì c= -2*-3 =6 (thỏa)
Vậy S= { (3;2;6) ; (-3;2;-6) ; (3;-2;-6) ; (-3;-2;6) }
Đúng 0
Bình luận (0)
Theo đề bài suy ra: \(ab.bc.ca=c.4a.9b\)
=>\(a^2.b^2.c^2=36abc\)
=>\(\left(abc\right)^2=36abc\)
=>\(\left(abc\right)^2:abc=36\)
=>\(abc=36\)
=>\(\hept{\begin{cases}ab=36:c\\ac=36:b\\bc=36:a\end{cases}}\)
Ta có:
ab=c => 36:c=c => c2=36 =>\(c\in\left\{-6;6\right\}\)bc=4a => 36:a=4a => 4a2=36 => a2=9 => \(a\in\left\{-3;3\right\}\)ac=9b => 36:b=9b => 9b2=36 => b2=4 => \(b\in\left\{-2;2\right\}\)Vậy .....
Đúng 0
Bình luận (0)
tim abc biet ab,c 2=a,bc+41,06
tim a;b;c >o biet ab=3/5; bc=4/5; ca=3/4. Tim a;b;c