cho tam giác ABC có \(\widehat{ABC}\)=135 độ AB=\(\sqrt{2}\)cm BC=\(2cm\).tính AC
Tam giác ABC có ABC=135 độ. BC=2cm. AB=\(\sqrt{2}\). Tìm AC
Tam giác ABC có ABC=135 độ. BC=2cm. AB=\(\sqrt{2}\). Tìm AC
Cho tam giác ABC có AB = 1 cm, AC = 2cm, góc ABC = 45 độ, góc ACB = 30 độ. Tính độ dài BC và diện tích tam giác ABC.
Cho tam giác ABC có \(\widehat{B}=30\);\(\widehat{C}=135\)và BC=2cm. Tính diện tích tam giác ABC
Cho tam giác ABC vuông tại A, BC= \(3\sqrt{5}\)cm. Hình vuông ADEF cạnh 2cm có D thuộc AB, E thuộc BC, F thuộc AC. Tính độ dài các cạnh AC, AB
Đặt \(\hept{\begin{cases}AB=x\\AC=y\end{cases}\left(x,y>0\right)}\)
Theo định lí Thales \(\frac{EF}{AB}=\frac{CF}{CA}\Rightarrow\frac{AB-EF}{AB}=\frac{CA-CF}{CA}\)
Hay \(\frac{x-2}{x}=\frac{2}{y}\Leftrightarrow xy=2\left(x+y\right)\left(1\right)\)
Theo định lí Pytagoras: \(AB^2+AC^2=BC^2\)hay \(x^2+y^2=45\left(2\right)\)
Từ (1),(2); ta có hệ phương trình: \(\hept{\begin{cases}xy=2\left(x+y\right)\\x^2+y^2=45\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\x^2+2xy+y^2-4\left(x+y\right)-45=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\\left(x+y\right)^2-4\left(x+y\right)-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=9\\x^2+y^2-45=0\end{cases}}\)(Vì x,y dương)
\(\Leftrightarrow\hept{\begin{cases}y=9-x\\x^2+\left(9-x\right)^2-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=9-x\\x=6\left(h\right)x=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\left(h\right)\hept{\begin{cases}x=3\\y=6\end{cases}}\)
Vậy \(AB=3,AC=6\) hoặc \(AB=6,AC=3.\)
Cho tam giác ABC có độ dài cạnh AC=1dm, nếu cạnh AC dài thêm 2cm nữa thì độ dài cạnh AC gấp 2 lần độ dài cạnh BC. Độ dài cạnh AB lớn hơn độ dài cạnh BC 2cm. Khi đó, chu vi hình tam giác ABC là ...(cm
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)
Cho tam giác ABC, hãy tính cạnh BC nếu biết:
1, AB=1cm, AC=2cm,\(\widehat{BAC}=120^o\)
2,AB=1dm, AC=5 cm,\(\widehat{BAC}=60^O\)
Bài 2. (2 điểm)
a) Tính độ dài x trong hình vẽ (Biết DE // BC )
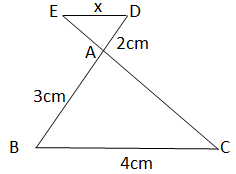
b. Cho tam giác ABC có AB = 2cm, AC = 3cm, BC = 4 cm, phân giác AD. Tính độ dài của BD và CD.
a | Áp dụng hệ quả của định lý Ta-lét ta có: 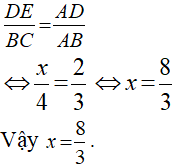 |
b | Ta có: 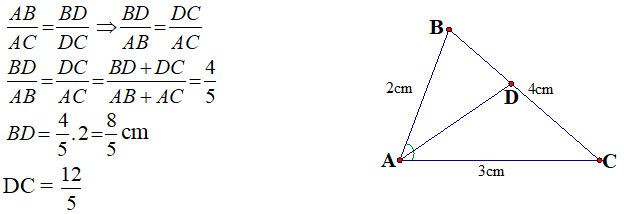 |
a | Áp dụng hệ quả của định lý Ta-lét ta có: 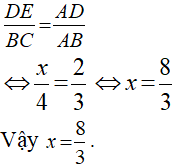 |
b | Ta có:  |