Cho tam giác ABC. các đường phân giác BD và CE biết AD/DC=2/3; AE/EB5/6. Tính các cạnh của tam giác biết chu vi của nó bằng 45 cm.
NT
Những câu hỏi liên quan
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3 , EA/EB = 5/6 . Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
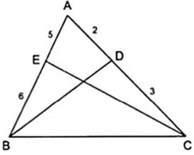
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
+ AB/BC = AD/DC = 2/3 = 4/6
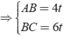 với t > 0
với t > 0
+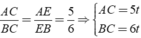
Theo giả thiết ta có: P A B C = A B + A C + B C = 15 t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 2
Bình luận (0)
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
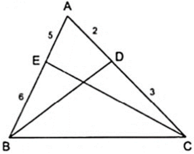
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
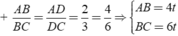 với t > 0
với t > 0
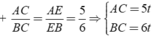
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
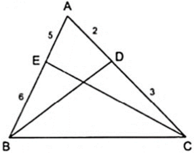
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
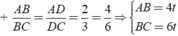 với t > 0
với t > 0
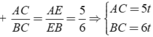
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường phân giác BD và CE. Biết\(\frac{AD}{DC}=\frac{2}{3}\), \(\frac{EA}{Eb}=\frac{5}{6}\) Tính các cạnh tam giác ABC biết chu vi tam giác bằng 45cm .
Cho Tam giác cân ABC (AB=AC) vẽ các đường phân giác BD và CE. a) CM BD=CE. b) CM ED//BC. c) biết AB=AC=6cm ; BC=4cm; hãy tính AD, DC, ED
Cho tam giác ABC có các đường phân giác BD và CE( \(D\in AC,E\in AB\)). Biết \(\frac{AD}{DC}=\frac{2}{3};\frac{AE}{EB}=\frac{5}{6}\), chu vi tam giác ABC là 45cm. Tính độ dài các cạnh của tam giác ABC.
Áp dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AB}{AD}=\frac{BC}{DC}\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{2}{3}\Rightarrow\frac{AB}{2}=\frac{BC}{3}\)(1)
Lại ap dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AC}{AE}=\frac{BC}{EB}\Rightarrow\frac{AC}{BC}=\frac{AE}{EB}=\frac{5}{6}\Rightarrow\frac{AC}{5}=\frac{BC}{6}\)(2)
Từ (1) và (2) suy ra \(\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{45}{15}=3\)
Vậy độ dài các cạnh của tam giác ABC lần lượt là 12;15;18 (cm)
Hình bạn tự vẽ nhé
Xét tam giác ABC có CE là đường phân giác của góc ACB (gt)
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}\)( tính chất đường phân giác trong của tam giác )
\(\Rightarrow\frac{AC}{BC}=\frac{5}{6}\)( Vì\(\frac{AE}{EB}=\frac{5}{6}\))
\(\Rightarrow6AC=5BC\)
Xét tam giác ABC có đường phân giác BD của góc ABC(gt)
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}\)( tích chất của đường phân giác trong của tam giác )
\(\Rightarrow\frac{AB}{BC}=\frac{2}{3}\)( Vì \(\frac{AD}{DC}=\frac{2}{3}\))
\(\Rightarrow3AB=2BC\)
Theo bài ra ta có: \(\hept{\begin{cases}6AC=5BC\\3AB=2BC\end{cases}}\)và \(AB+BC+CA=45\)
\(\Rightarrow\hept{\begin{cases}\frac{AC}{5}=\frac{BC}{6}\\\frac{AB}{4}=\frac{BC}{6}\end{cases}}\)
\(\Rightarrow\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{AB+AC+BC}{4+5+6}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}AB=3.4=12\left(cm\right)\\AC=3.5=15\left(cm\right)\\BC=3.6=18\left(cm\right)\end{cases}}\)
Vậy ...
+) Xét tam giác ABC có : CE là đường phân giác ( GT )
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}=\frac{5}{6}\)( T/c đường phân giác trong tam giác )
\(\Rightarrow5BC=6AC\)
Tương tự xét tam giác ABC có BD là phân giác ( GT )
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}=\frac{2}{3}\)
\(\Rightarrow2BC=3AB\)
Ta có :
\(\hept{\begin{cases}5BC=6AC\\2BC=3AB\end{cases}}\)(1) và \(AB+AC+BC=45\)( Do diện tích tam giác ABC = 45cm )
Từ ( 1 )
\(\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{3}=\frac{AB}{2}\end{cases}\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{6}=\frac{AB}{4}\end{cases}\Leftrightarrow}}\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}\)
Áp dụng TC của dãy tỉ số bằng nhau , ta có :
\(\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}=\frac{BC+AC+AB}{6+5+4}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}BC=18\\AC=15\\AB=12\end{cases}}\)
P/s : Bạn Châu sai chỗ nào zậy ?? k sai bừa !!
Xem thêm câu trả lời
Cho tam giác ABC, AB=8cm, AC=10cm, BC=12cm. Các đường phân giác BD và CE cắt nhau tại I. Tính AD, DC, AE, BE
Áp dụng định lý phân giác ta có:
\(\dfrac{AD}{DC}=\dfrac{AB}{AC}=\dfrac{4}{5}\Rightarrow\dfrac{AD}{4}=\dfrac{DC}{5}=\dfrac{AD+DC}{4+5}=\dfrac{10}{9}\)
\(\dfrac{AD}{4}=\dfrac{10}{9}\Rightarrow AD=\dfrac{40}{9}\left(cm\right)\\ \dfrac{DC}{5}=\dfrac{10}{9}\Rightarrow DC=\dfrac{50}{9}\)
Áp dụng định lý phân giác ta có:
\(\dfrac{AE}{EB}=\dfrac{AC}{BC}=\dfrac{5}{6}\Rightarrow\dfrac{AE}{5}=\dfrac{EB}{6}=\dfrac{AE+EB}{5+6}=\dfrac{8}{11}\)
\(\dfrac{AE}{5}=\dfrac{8}{11}\Rightarrow AE=\dfrac{40}{11}\left(cm\right)\\ \dfrac{EB}{6}=\dfrac{8}{11}\Rightarrow EB=\dfrac{48}{11}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB = 4cm, BC=6cm, AC=5cm, các đường phân giác BD và CE cắt nhau tại I.
a) Tính AD, DC
b) Tính tỉ số diện tích 2 tam giác DIE và ABC
a, Theo tính chất đường phân giác ta có : \(\frac{AD}{AB}=\frac{DC}{BC}\)=> \(\frac{AD}{4}=\frac{DC}{6}\)=> \(\frac{AD}{2}=\frac{DC}{3}=\frac{AD+DC}{2+3}=\frac{AC}{5}=\frac{5}{5}=1\)
=> \(\hept{\begin{cases}AD=2\\DC=3\end{cases}}\)
Đúng 2
Bình luận (0)
a) Áp dụng tính chất đường phân giác ta có:
\(\frac{AD}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{2}{3}\)
\(\Leftrightarrow\frac{AD}{2}=\frac{AB}{3}=\frac{AD+AB}{2+3}=1\)
\(\Leftrightarrow AD=2;AB=3\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho △ABC có AB= 4cm, AC= 5cm, BC= 6cm, các đường phân giác BD và CE cắt
nhau ở I.
a) Tính AD, DC.
b) Tính tỉ số diện tích các tam giác DIE và ABC.









