cho P =|x|.(y-1).Tim x,y thuoc Z biet P<0
NL
Những câu hỏi liên quan
Cho A thuoc {0.1.2.3.4.5.6.7.8.9.10} biet A co hon 1 phan tu neu x,y,z thuoc A va x<y<z thi z =x.y tim A
tim x ,y thuoc z biet: (x-1)(x+y) =32
(x-1)(x+y) = 32
=> x-1 và x+y thuộc Ư(32)
Kẻ bảng xét các trường hợp của x-1 và x+y là ra
Đúng 0
Bình luận (0)
Tim x, y thuoc Z biet : | x-2| + (x-y+1)^2 =0
Có 2 Th | x-2| , (x-y+1)^2 =0
| x-2| , (x-y+1)^2 là hai số đối ; lx-2/ nguyên dương => ( x - y + 1 )^2 là số nguyên âm
TH1 | x-2| , (x-y+1)^2 =0
=> x = 2 để /x-2/ = 0
thay vào bên kia ta có : ( 2 - y + 1 ) ^2 = 0 => 2 - y + 1 = 0 => 3 - y = 0 => y = 3
TH2 : Tự xét nha bn
Đúng 0
Bình luận (0)
tim x;y thuoc z biet:
1/x + 1/y = 1/5
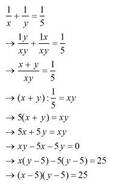
Ta xét:
\(\left(x-5\right)\left(y-5\right)=25\Leftrightarrow x-5=y-5=5\Leftrightarrow x=y=10\)
\(x-5=y-5=-5\Leftrightarrow x=y=0\)
\(\left\{{}\begin{matrix}x-5=1\\y-5=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=30\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-1\\y-5=-25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\y=-20\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=25\\y-5=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=30\\y=6\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-25\\y-5=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-20\\y=4\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(10;10\right),\left(0;0\right),\left(6;30\right),\left(4;-20\right),\left(30;6\right),\left(-20;4\right)\right\}\)
Đúng 0
Bình luận (0)
tim x, y thuoc z biet :
/ x-y / + / y-z/ + /z - x / = 2015
tim cac so x,y,z thuoc Q biet rang (x+y):(5-z):(y+z):(y+9)=3:1:2:5
Ta có:(x+y):(5-z):(y+z):(y+9)=3:1:2:5
=> 5-z=1=>z=4.
y+9=5=>y=-4.
x+y=3=>x-4=3(do y=-4)=>x=7.
Vậy x=7,y=-4,z=4.
Đúng 0
Bình luận (0)
tim x,y thuoc Z biet x*y=x+y
Xem thêm câu trả lời
tim x,y,z thuoc z biet /x/+/y/+/z/=0
VÌ \(\left|x\right|\ge0;\left|y\right|\ge0;\left|z\right|\ge0\)NÊN ĐỂ\(\left|x\right|+\left|y\right|+\left|z\right|=0\)\(\Leftrightarrow\hept{\begin{cases}\left|x\right|=0\\\left|y\right|=0\\\left|z\right|=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=0\\z=0\end{cases}}}\)
Đúng 0
Bình luận (0)
Tim x, y thuoc Z, biet:
x.y+x+y+1=-3
xy+x+y+1=-3
x(y+1)+y+1=-3
=>(y+1)(x+1)=-3
=> y+1 ;x+1 thuộc Ư(3)={ \(\pm1;\pm3\)}
th1: y+1=-1;x+1=3
y+1=-1
=>y=-2
x+1=3
=>x=2
th2: y+1=1;x+1=-3
y+1=1
=> y=0
x+1=-3
=>x=-4
vậy....


