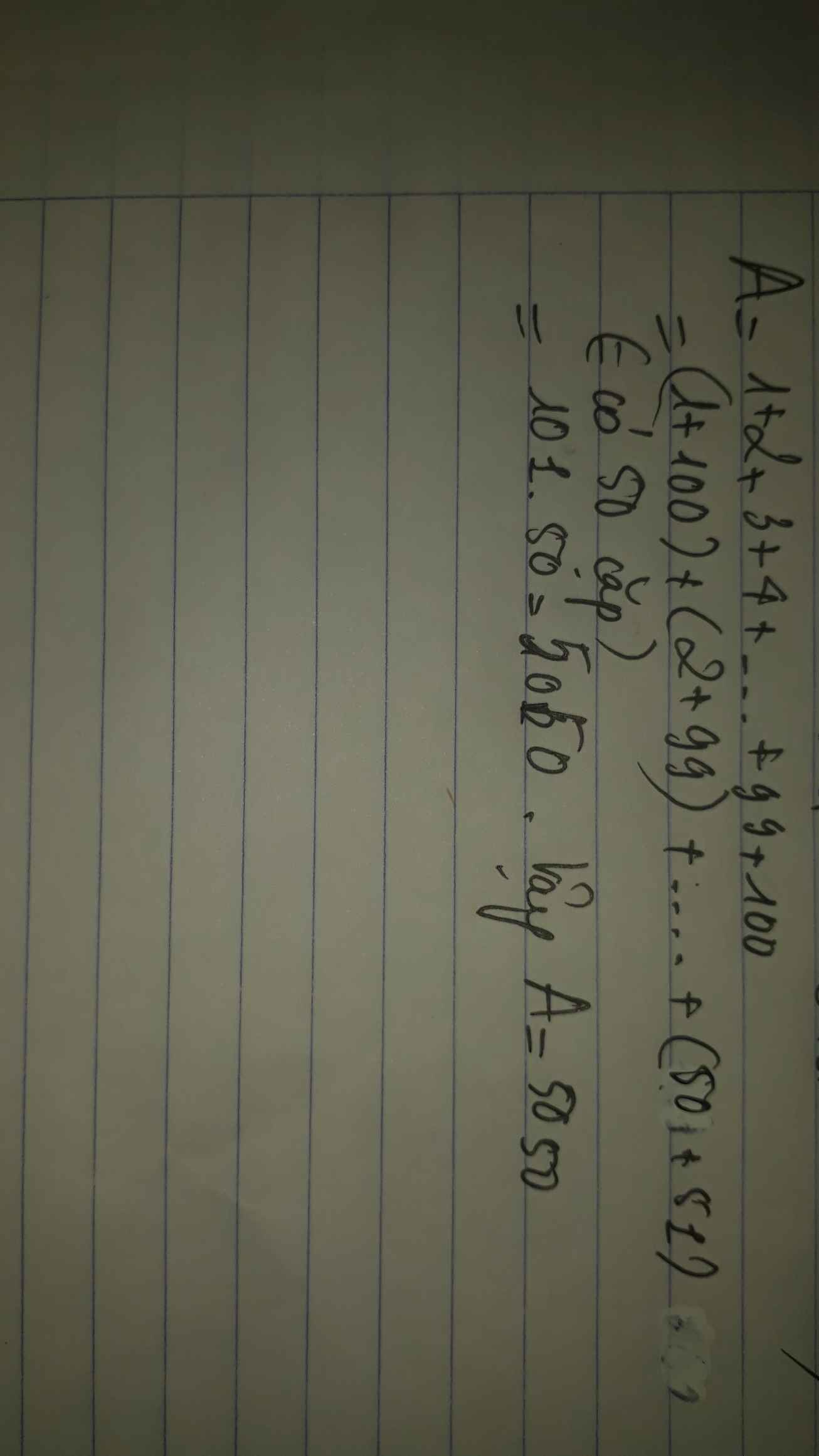Tính tổng: A=1+2+3+...+99+100
NL
Những câu hỏi liên quan
Tính tổng:
a) A= 1^2*2 + 2^2 *3 + 3^2*4 +...+ 99^2*100
b) B= 1*2^2 + 2*3^2 + 3*4^2 +...+ 99*100^2
c) C= 1^3 + 2^3 + 3^3 +...+ 99^3
Tính tổng:
\(A=1+3+3^2+3^3+...+3^{99}+3^{100}\)100
\(B=1-2+2^2-2^3+2^4-...-2^{99}+2^{100}\)
\(A=1+3+3^2+...+3^{100}\)
\(\Rightarrow3A=3+3^2+3^3+...+3^{101}\)
\(\Rightarrow3A-A=3^{101}-1\)
\(\Rightarrow A=\frac{3^{101}-1}{2}\)
Đúng 0
Bình luận (0)
tính tổng
a) 1 - 2 + 3 - 4 + ... + 99 - 100
b) 2 - 4 + 6 - 8 + ... + 48 - 50
c) -1 + 3 - 5 + 7 - ... + 97 - 99
d) 1 + 2 - 3 - 4 + ... + 97 + 98 - 99 -100
Tớ chỉ làm câu a thôi nhé !
a) 1-2+3-4+........+99-100 ( 100 số số hạng)
=(1-2)+(3-4)+........+(99-100) (50 cặp)
=(-1)+(-1)+............+(-1)
=(-1)*50
=(-50)
Dấu * có nghĩa là dấu nhân nhé !
Mình không chắc về đáp án này lắm đâu !
Đúng 0
Bình luận (0)
a)Bán áp dụng tính giao hoán sẽ ra kết quả nhanh chóng.
Ta sẽ giao hoán như sau:
1+ 3-2 + 5-4 + 7-6 + ... + 99-98 - 100 =
1 + (1 + 1 + 1 + 1 + 1 + ... + 1) - 100 =................(trong ngoặc có 49 số 1 vì 49 x 2 + 1 =99)
= 1 + 49 - 100 = âm 50.
Hoặc có cách này:
1 + 3 + 5 + ... + 97 + 99 - (2 + 4 + 6 + ... + 100) = - 50.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính tổng sau:
\(A=\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+....+\frac{1}{100\sqrt{99}+99\sqrt{100}}\)
tính tổng dãy số A = 1+2+3+4+....+99+100
Xem thêm câu trả lời
Tính tổng sau đây một cách hợp lý
a,1-2+3-4+.....+99-100
b.1+2-3-4+5+6-......+97+98-99-100
a, 1-2+3-4+...+99-100
= (1-2)+(3-4)+...+(99-100)
= -1 + (-1) +...+ (-1)
= -1 x 50
= -50
b, 1+2-3-4+5+6-...+97+98-99-100
= (1+2-3-4) + (5+6-7-8) + ... + (97+98-99-100)
= -4 +( -4) + .... + (-4)
= -4 x 25
= -100
Tính tổng
a) -1+3-5+7-...+97-99
b) 1+2-3-4+...+97+98-99-100
bạn có thể trình bày ra cho mình k
Đúng 0
Bình luận (0)
Tính tổng
a)1+2-3-4+5+6-7-8+.......+2021+2022
b)100+98+99+94+........+2-99-97-95-....-1
1/
$A=1+2-3-4+5+6-7-8+....+2017+2018-2019-2020+2021+2022$
$=(1+2-3-4)+(5+6-7-8)+...+(2017+2018-2019-2020)+4043$
$=(-4)+(-4)+(-4)+...+(-4)+4043$
Số lần xuất hiện của -4 là: $[(2020-1):1+1]:4=505$
$A=(-4)\times 505+4043=2023$
Đúng 0
Bình luận (0)
Câu b có vẻ đề sai. Bạn xem lại nhé.
Đúng 0
Bình luận (0)
Tính tổng A biết:
A 1*2+2*3+3*4+...+99*100
A = 1 x 2 + 2 x 3 + 3 x 4 + ... + 99 x 100
3A = 1 x 2 x 3 + 2 x 3 x ( 4 - 1 ) + 3 x 4 x ( 5 - 2 ) + .... + 99 x 100 x ( 101 - 98 )
3A = 1 x 2 x 3 + 2 x 3 x 4 - 1 x 2 x 3 + ... + 99 x 100 x 101 - 98 x 99 x 100
3A = 99 x 100 x 101
3A = 999900
A = 999900 : 3
A = 333300
Đúng 0
Bình luận (0)
S = 1 x 2 + 2 x 3 + ... + 99 x 100
3S = 1 x 2 x 3 + 2 x 3 x (4 - 1) + ..... + 99 x 100 x (101 - 98)
3S = 1 x 2 x 3 + 2 x 3 x 4 - 1 x 2 x 3 + .... + 99 x 100 x 101 - 98 x 99 x 100
3S = 99 x 100 x 101 = 999900
S = 999900 : 3 = 333300
Đúng 0
Bình luận (0)