biểu diễn số hữu tỉ -5/4; -8/-8; 7/5; 4/-3 trên trục số
NK
Những câu hỏi liên quan
1.Biểu diễn các số hữu tỉ \(\dfrac{-3}{4}\); \(\dfrac{5}{3}\) trên trục số .
2. So sánh hai số hữu tỉ -0.75 và \(\dfrac{5}{3}\)
1)mik ko biết trục số ở đâu nên tham khảo:
2
-0,75 <5/3
Đúng 0
Bình luận (0)
Biểu diễn số hữu tỉ 1và1/3; 2và .5/6; 4; 4,và 5 trên trục số
Để biểu diễn các số hữu tỉ trên trục số, chúng ta sẽ sử dụng một đường thẳng và các điểm trên đường thẳng đại diện cho các số hữu tỉ tương ứng.
1 và 1/3: Đặt điểm 1 trên trục số, sau đó từ điểm 1, di chuyển một phần ba đơn vị về bên phải để đặt điểm 1/3.
2 và 5/6: Đặt điểm 2 trên trục số, sau đó từ điểm 2, di chuyển năm phần sáu đơn vị về bên phải để đặt điểm 5/6.
4: Đặt điểm 4 trên trục số.
4 và 5: Đặt điểm 4 và 5 lên trục số.
Sau khi đặt các điểm này, chúng ta có thể kết nối các điểm trên trục số bằng đường thẳng để biểu diễn các số hữu tỉ tương ứng.
Đúng 0
Bình luận (0)
biểu diễn các số hữu tỉ : 3/-4, 5/3
Biểu diễn các số hữu tỉ : 3 / -4 ; 5/3
Bài 1: Đề như đã sửa thì cách giải như sau:
Trong Tam giác ABC
Có AM/AB = AN/AC
Suy ra: MN // BC .
Trong tam giác ABI
có
MK // BI do K thuộc MN
Do đó : MK/BI =AM/AB (1)
Tương tự trong tam giác AIC
Có NK// IC nên NK/IC = AN/AC (2)
Từ (1) (2) có NK/IC = MK/BI do AN/AC = AM/AB
Lại có IC = IB ( t/c trung tuyến)
nên NK = MK (ĐPCM)
Bài 2:
Bài này thứ tự câu hỏi hình như ngược mình giải lần lượt các câu b) d) c) a)
Từ A kẻ đường cao AH ( H thuộc BC).
b) Do tam giác ABC vuông tại A áp dụng pitago ta có
BC=căn(AB mũ 2 + AC mũ 2)= 20cm
d) Có S(ABC)= AB*AC/2= AH*BC/2
Suy ra: AH= AB*AC/ BC = 12*16/20=9.6 cm
c) Ap dung định lý cosin trong tam giác ABD và ADC ta lần lượt có đẳng thức:
BD^2= AB^2 + AD^2 - 2*AB*AD* cos (45)
DC^2= AC^2+ AD^2 - 2*AC*AD*cos(45) (2)
Trừ vế với vế có:
BD^2-DC^2=AB^2-AC^2- 2*AB*AD* cos (45)+2*AC*AD*cos(45)
(BC-DC)^2-DC^2 = -112+4*Căn (2)* AD.
400-40*DC= -112+................
Suy 128- 10*DC= Căn(2) * AD (3)
Thay (3) v ào (2): rính được DC = 80/7 cm;
BD= BC - DC= 60/7 cm;
a) Ta có S(ABD)=AH*BD/2
S(ADC)=AH*DC/2
Suy ra: S(ABD)/S(ACD)= BD/DC = 60/80=3/4;
Đúng 0
Bình luận (0)
biểu diễn số hữu tỉ trên trục số
biểu diễn:5/2,-7/2,5/-2,-4/-2
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
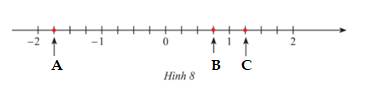
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

Đúng 0
Bình luận (0)
Biểu diễn các số hữu tỉ 3/-4 ; 5/3 trên trục số
x + 25 = 64
x = 64 - 25
x = 39
Vậy x = 39
Đúng 0
Bình luận (0)
=> x + 25 = 64
=>x = 64 - 25
=>x = 39
Vậy x =39
Đúng 0
Bình luận (0)
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
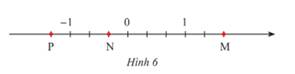
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)

Đúng 0
Bình luận (0)
Điểm P biểu diễn: \(-\dfrac{4}{3}\)
Điểm N biểu diễn: \(-\dfrac{1}{3}\)
Điểm M biểu diễn: \(\dfrac{5}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Biểu diễn các số hữu tỉ 3/-4, 5/3 trên trục số
biểu diễn các số hữu tỉ sau trên trục số 5/3 và -3/4
Biểu diễn trên trục số như sau :






