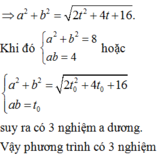Đáp án D

Lời giải:

Đặt  t = x − 512 1024 − x 8 ≥ 0 , ta có

t 4 = x − 512 1024 − x ≤ x − 512 + 1024 − x 2                                                                                                 = 256 ⇒ 0 ≤ t ≤ 4

Với t = 4 thì ta tìm được 1 giá trị của x = 768

Với 0 ≤ t ≤ 4  thì ta tìm được 2 giá trị của x (Khi đó phương trình của Định lý Viét đảo có 2 nghiệm phân biệt)

Bình phương 2 vế phương trình đã cho, ta được

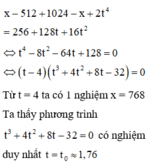
(sử dụng máy tính).

Từ đó ta có 2 nghiệm x thỏa mãn 

Do đó phương trình đã cho có 3 nghiệm.

Chọn đáp án C.

Đáp án C

x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 (*),  512 ≤ x ≤ 1024

t = x - 512 1024 - x 8 ⇒ t 4 = x - 512 1024 - x     ≤ x - 512 + 1024 - x 2 = 256 ⇒ 0 ≤ t ≤ 4   t = 4 ⇒ x = 768 0 ≤ t ≤ 4  

=> Bình phương hai vế (*):

( t - 4 ) t 3 + 4 t 2 + 8 t - 32 = 0 ⇔ [ x ≈ 512 , 18 x ≈ 1023 , 82

Đáp án C

x − 512 + 1024 − x = 16 + 4 ( x − 512 ) ( 1024 − x ) 8     ( * ) , ( 512 ≤ x ≤ 1024 ) t = ( x − 512 ) ( 1024 − x ) 8 ⇒ t 4 = ( x − 512 ) ( 1024 − x ) ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4 ⋅ t = 4 ⇒ x = 768

0 ≤ t < 4 ⇒ bình phương 2 vế (*):

⇒ ( t − 4 ) ( t 3 + 4 t 2 + 8 t − 32 ) = 0 ⇔ t ≈ 1 , 76 ⇔ x ≈ 512 , 18 x ≈ 1023 , 82

x^20-x=0

x(x^19-1)=0

x= 0 

hoặc x ^ 19 =1

x = 0 hoặc x= 1

\(\dfrac{x}{1024}=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+...-\dfrac{1}{1024}\)

\(\dfrac{2x}{1024}=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+...-\dfrac{1}{512}\)

\(\Rightarrow\dfrac{x}{1024}+\dfrac{2x}{1024}=1-\dfrac{1}{1024}\)

\(\Rightarrow\dfrac{3x}{1024}=\dfrac{1023}{1024}\)

\(\Rightarrow3x=1023\)

\(\Rightarrow x=341\)

Lời giải:

$\frac{x}{1024}=\frac{1}{2}-\frac{1}{4}+\frac{1}{8}-\frac{1}{16}+...-\frac{1}{1024}$

$\frac{2x}{1024}=1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+...-\frac{512}$

$\Rightarrow \frac{x}{1024}+\frac{2x}{1024}=1-\frac{1}{1024}$

$\frac{3x}{1024}=\frac{1023}{1024}$

$\Rightarrow 3x=1023$

$\Rightarrow x=341$

17 quyen

khong biet dung khong

\(B=\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{64}+...+\dfrac{1}{1024}\)

\(4B=1+\dfrac{1}{4}+\dfrac{1}{16}+...+\dfrac{1}{256}\)

\(4B-B=1-\dfrac{1}{1024}\)

\(3B=\dfrac{1023}{1024}\)

\(B=\dfrac{1023}{1024}:3\)

\(B=\dfrac{341}{1024}\)

B=1/4+1/16+1/64+..+1/1024

B=1/4+1/4^2+1/4^3+....+1/4^5

4B=1+1/4^2+....+1/4^4

=>4B-B=1-1/4^5

=>3B=1-1/4^5

=>B=1/3-1/(4^5*3)

Đặt $A=\dfrac12+\dfrac14+\dfrac18+\dfrac{1}{16}+...+\dfrac{1}{1024}$

$A=\dfrac12+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{10}}$

$\dfrac12\cdot A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+...+\dfrac{1}{2^{11}}$

$A-\dfrac{1}{2}A=(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{10}})-(\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+...+\dfrac{1}{2^{11}})$

$\dfrac{1}{2}A=\dfrac{1}{2}-\dfrac{1}{2^{11}}$

$\dfrac{1}{2}A=\dfrac{1}{2}\cdot(1-\dfrac{1}{2^{10}})$

$\Rightarrow A=1-\dfrac{1}{2^{10}}$

Vậy: ...

$Toru$