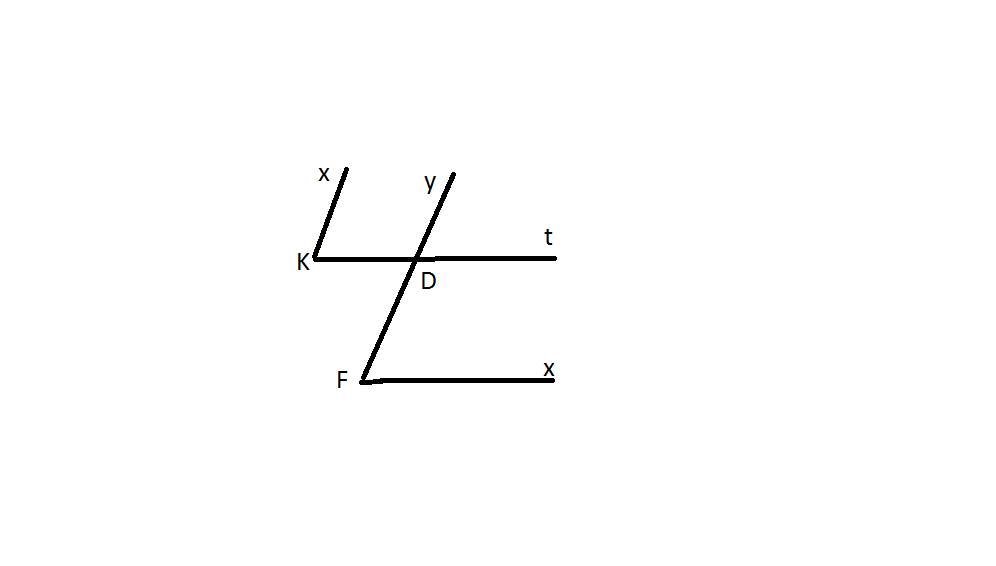
a,Tìm các góc so le trong với KDF
b,Tìm 1 góc đồng vị với yDt
gấp ạ
Cho Hình 3.28.
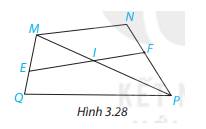
a) Tìm các góc ở vị trí so le trong với góc FIP; NMI
b) Tìm các góc ở vị trí đồng vị với góc EQP; IFP.
a) Góc ở vị trí so le trong với góc FIP là góc IPQ
Góc ở vị trí so le trong với góc NMI là góc MIE và góc MPQ.
b) Góc ở vị trí đồng vị với góc EQP là góc MEF
Góc ở vị trí đồng vị với góc IFP là góc MNP
cho hình vẽ
a. tìm các góc so le trong, so le ngoài, đồng vị.
b. cho góc A2 = 70 độ, B1 = 110 độ. tìm các góc còn lại.
c. đường thẳng a có song song với b hay không ? vì sao?
Quan sát hình 3.24.
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
d) Biết MN//BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ
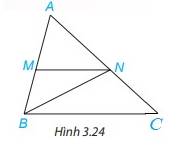
a) Góc MNB so le trong với góc NBC
b) Góc ACB đồng vị với góc ANM
c) Các cặp góc trong cùng phía là: góc MNC và góc NCB; góc NMB và góc MBC
d) Vì MN//BC nên
\(\widehat {ANM} = \widehat {ACB}\) (2 góc đồng vị)
\(\widehat {AMN} = \widehat {ABC}\) (2 góc đồng vị)
\(\widehat {MNB} = \widehat {NBC}\) ( 2 góc so le trong)
Cho hai đường thẳng a, b song song với nhau, câu nào là sai ?
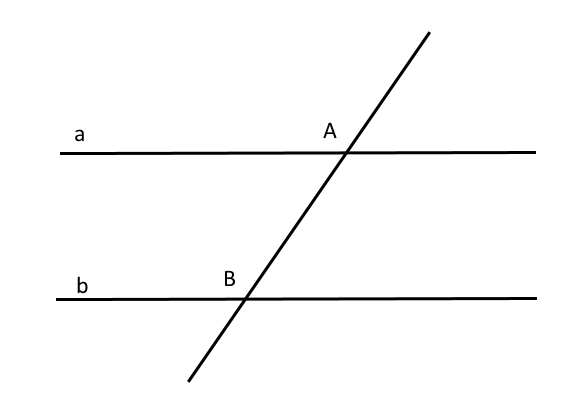
A. Hai góc trong cùng phía bù nhau, hai góc đồng vị bằng nhau
B. Hai góc đồng vị bằng nhau, hai góc so le trong bù nhau
C. Hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau
D. Hai góc trong cùng phía bù nhau, hai góc so le trong bằng nhau
B. Hai góc đồng vị bằng nhau, hai góc so le trong bù nhau
B nha vì 2 góc so le trong phải bằng nhau
a) tìm 1 góc so le trong với góc HKN
b) tìm 1 góc đồng vịvới góc MKH
c) kể tên 2 cặp góc trong cùng phía
d) biết Hk song song MN . hãy kể tên 3 cặp góc bằng nhau
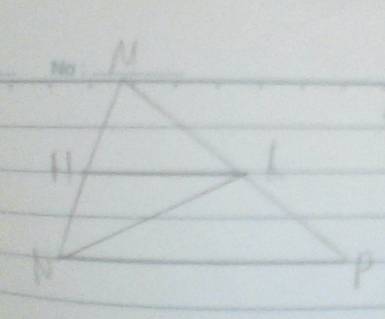
a) Để tìm một góc so le với góc HKM, chúng ta có thể chọn góc KHN. b) Để tìm một góc đồng vị với góc MKH, chúng ta có thể chọn góc HKM. c) Có hai cặp góc trong cùng phía, đó là cặp góc HKM và góc KHN, cũng như cặp góc MKH và góc KHN. d) Với điều kiện HK song song với MN, ta có thể kể tên ba cặp góc bằng nhau là góc HKM và góc MHN, góc KHN và góc MNH, cũng như góc MKH và góc NHM
cho góc yon 50 độ. Vẽ góc mox đối đỉnh với yon. Lấy điểm a thuộc tia ox. Kẻ tia At song song với dường thẳng mn. Tìm cá cặp góc so le trong, đồng vị, trong cùng phía có trên hình vẽ
Các cặp góc đối đỉnh : yON và MOA ; MOy và NOA
( theo đề là At // MN về 1 phía nhé )
Các cặp góc so le trong : MOA và OAt ; yON và OAt ;NOA và TAx
Các cặp góc trong cùng phía : NOA và OAt
A/ Vẽ 1 đường thẳng cắt 2 đường thẳng. Trong các góc tạo thành có 1 cặp góc so le trong = nhau. Đặt tên cho các góc đó.
b/ vì sao cặp góc so le trong còn lại cũng = nhau?
c/ vì sao mỗi cặp góc đồng vị = nhau?
d/ vì sao mỗi cặp góc trong cùng phía bù nhau?
e/ vì sao mỗi cặp góc ngoài cùng phía bù nhau?
Em làm đc câu a,b rồi ạ. Mong mn giúp em câu c,d,e với ạ! Em cám ơn mn❤️
Xem hình 3.5 rồi cho biết góc nào so le trong, đồng vị, trong cùng phía:
a) Với góc ADC
b) Với góc BAC
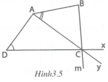
a) Xét hai đường thẳng AD và Bm, đối với cát tuyến Dx thì:
- Góc DCm so le trong với góc ADC;
- Góc BCx đồng vị với góc ADC;
- Góc DCB trong cùng phía với góc ADC.
b) Xét hai đường thẳng AB và Dx, đối với cát tuyến Ay thì:
- Góc ACD so le trong với góc BAC;
- Góc xCy đồng vị với góc BAC;
- Góc Acx trong cùng phía với góc BAC.
Vận dụng cặp góc so le trong
 Bài 3: (3,25 điểm) Vẽ lại hình sau
Bài 3: (3,25 điểm) Vẽ lại hình sau
a) Hãy cho biết: Góc đồng vị với ![]() ; Góc so le trong với
; Góc so le trong với ![]() ; Góc trong cùng phía với
; Góc trong cùng phía với ![]() là góc nào?
là góc nào?
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
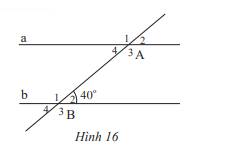
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)