Cho hình vẽ: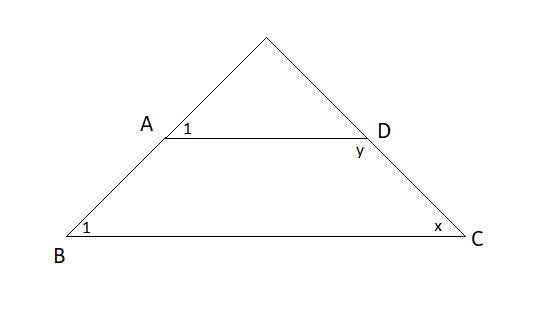
Biết góc \(A_1=\) góc \(B_1\)
và \(3x=2y\)
Tìm \(x,y\)
Giúp em với ạ...
Trên (P)lấy hai điểm A_1,A_2 lên sao cho góc (A_1 OA_2 ) ̂=90 độ (O là góc tọa độ).Hình chiếu vuông góc của A_1,A_2 lên trục hoành là B_1,B_2.Chứng minh rằng OB_1.OB_2=1
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
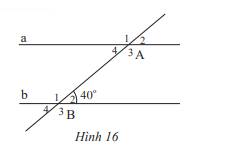
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\)
a) Tìm các giao điểm \({A_1},{A_2}\) của (E) với trục hoành và các giao điểm \({B_1},{B_2}\) của (E) với trục tung. Tính \({A_1}{A_2},{B_1}{B_2}\).
b) Xét một điểm bất kì \(M\left( {{x_o};{y_o}} \right)\) thuộc (E).
Chứng minh rằng, \({b^2} \le x_o^2 + y_o^2 \le {a^2}\) và \(b \le OM \le a\).
Chú ý: \({A_1}{A_2},{B_1}{B_2}\)tương ứng được gọi là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b.
a) Các giao điểm của (E) với trục hoành có tọa độ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \pm a\\y = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{A_1}\left( { - a;0} \right)\\{A_2}\left( {a;0} \right)\end{array} \right.\)
Các giao điểm của (E) với trục tung có tọa độ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = \pm b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{B_1}\left( {0; - b} \right)\\{B_2}\left( {0;b} \right)\end{array} \right.\)
Ta có \({A_1}{A_2} = 2a,{B_1}{B_2} = 2b\).
b) Do M thuộc (E) nên ta có \(\frac{{x_o^2}}{{{a^2}}} + \frac{{y_o^2}}{{{b^2}}} = 1\)
Do \(a > b > 0\) nên ta có \(\frac{{x_o^2}}{{{a^2}}} \le \frac{{x_o^2}}{{{b^2}}}\). Suy ra \(1 \le \frac{{x_o^2}}{{{b^2}}} + \frac{{y_o^2}}{{{b^2}}} \Rightarrow {b^2} \le x_o^2 + y_o^2\)
Tương tự ta có \(\frac{{y_o^2}}{{{a^2}}} \le \frac{{y_o^2}}{{{b^2}}}\) nên \(1 \ge \frac{{y_o^2}}{{{a^2}}} \le \frac{{y_o^2}}{{{b^2}}} \Rightarrow {a^2} \ge x_o^2 + y_o^2\)
Vậy \({b^2} \le x_o^2 + y_o^2 \le {a^2}\)
Ta có \(OM = \sqrt {x_o^2 + y_o^2} \) suy ra \(b \le OM \le a\)
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
cho parabol (P) \(y=x^2\) và 2 điểm\(A_1,A_2\) trên (P) sao cho góc \(A_1OA_2=90đ\) Gọi hình chiếu của\(A_1,A_2\) trên Ox lần lượt là \(B_1,B_2\). CM \(OB_1.OB_2=1\)
Cho đường thẳng d : 3x-2y+1=0 và M(1;2)
) Viết phương trình qua M và tạo với d một góc 45o. (đừng giải kiểu y=ax+b ạ) giúp emm ạ chi tiết
gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \)và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\)
+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\)
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\)
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)
Cho góc nhọn Xoy điểm M và N nằm trong góc Xoy sao cho hai tia OM, ON phân biệt.Hãy kể tên các góc trong hình vẽ. Tìm hai số nguyên x,y biết:xy-3x-2y=11
Tìm x và y biết:
-5x=-2y và -3x-4y=-208
x=
y=
Giúp với ạ
Theo đề bài, ta có:
x2=y3;y4=z5⇒x2=y3;y4=z5⇒x8=y12;y12=z15x8=y12;y12=z15⇒x8=y12=z15⇒x8=y12=z15
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x8=y12=z15=x+y−z8+12−15=105=2x8=y12=z15=x+y−z8+12−15=105=2
⇒⎧⎪ ⎪⎨⎪ ⎪⎩x8=2⇒x=16y12=2⇒y=24z15=2⇒z=30
B1 : 2 đường thẳng AB và CD cắt nhau tại O . Biết góc AOC + góc BOD = 130 độ . Tính số đo 4 góc tạo thành ? ( VẼ HÌNH GIÚP EM VỚI Ạ )
B2 : Cho 2 đường thẳng xx' và yy' cắt nhau tại O . Biết góc xOy = 60 độ : ( VẼ HÌNH GIÚP EM VỚI Ạ )
a, Tính số đo các góc còn lại ?
b , Vẽ tia phgiác om của góc xOy , tia phgiác on của góc x'Oy' . 2 2 tia om và on có phải là 2 tia đối nhau k ? Vì sao ?
Mn làm giúp em với ạ , em cảm ơn .