Cho hình vẽ:
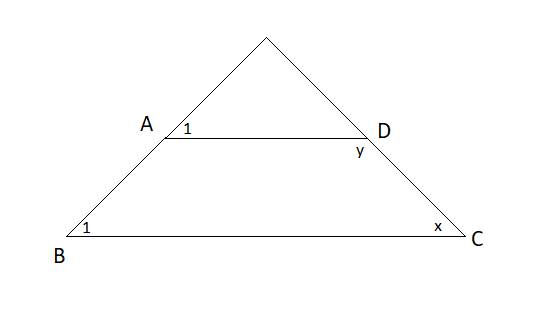
Biết góc \(A_1\) = góc \(B_1\)
và \(3x=2y\)
Tìm \(x,y\)
Trên (P)lấy hai điểm A_1,A_2 lên sao cho góc (A_1 OA_2 ) ̂=90 độ (O là góc tọa độ).Hình chiếu vuông góc của A_1,A_2 lên trục hoành là B_1,B_2.Chứng minh rằng OB_1.OB_2=1
cho parabol (P) \(y=x^2\) và 2 điểm\(A_1,A_2\) trên (P) sao cho góc \(A_1OA_2=90đ\) Gọi hình chiếu của\(A_1,A_2\) trên Ox lần lượt là \(B_1,B_2\). CM \(OB_1.OB_2=1\)
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
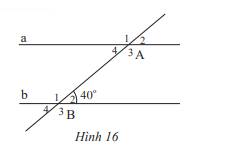
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Cho elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\)
a) Tìm các giao điểm \({A_1},{A_2}\) của (E) với trục hoành và các giao điểm \({B_1},{B_2}\) của (E) với trục tung. Tính \({A_1}{A_2},{B_1}{B_2}\).
b) Xét một điểm bất kì \(M\left( {{x_o};{y_o}} \right)\) thuộc (E).
Chứng minh rằng, \({b^2} \le x_o^2 + y_o^2 \le {a^2}\) và \(b \le OM \le a\).
Chú ý: \({A_1}{A_2},{B_1}{B_2}\)tương ứng được gọi là trục lớn, trục nhỏ của elip (E) và tương ứng có độ dài là 2a, 2b.
a) Các giao điểm của (E) với trục hoành có tọa độ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \pm a\\y = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{A_1}\left( { - a;0} \right)\\{A_2}\left( {a;0} \right)\end{array} \right.\)
Các giao điểm của (E) với trục tung có tọa độ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = \pm b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{B_1}\left( {0; - b} \right)\\{B_2}\left( {0;b} \right)\end{array} \right.\)
Ta có \({A_1}{A_2} = 2a,{B_1}{B_2} = 2b\).
b) Do M thuộc (E) nên ta có \(\frac{{x_o^2}}{{{a^2}}} + \frac{{y_o^2}}{{{b^2}}} = 1\)
Do \(a > b > 0\) nên ta có \(\frac{{x_o^2}}{{{a^2}}} \le \frac{{x_o^2}}{{{b^2}}}\). Suy ra \(1 \le \frac{{x_o^2}}{{{b^2}}} + \frac{{y_o^2}}{{{b^2}}} \Rightarrow {b^2} \le x_o^2 + y_o^2\)
Tương tự ta có \(\frac{{y_o^2}}{{{a^2}}} \le \frac{{y_o^2}}{{{b^2}}}\) nên \(1 \ge \frac{{y_o^2}}{{{a^2}}} \le \frac{{y_o^2}}{{{b^2}}} \Rightarrow {a^2} \ge x_o^2 + y_o^2\)
Vậy \({b^2} \le x_o^2 + y_o^2 \le {a^2}\)
Ta có \(OM = \sqrt {x_o^2 + y_o^2} \) suy ra \(b \le OM \le a\)
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \)và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\)
+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\)
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\)
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
Cho góc nhọn Xoy điểm M và N nằm trong góc Xoy sao cho hai tia OM, ON phân biệt.Hãy kể tên các góc trong hình vẽ. Tìm hai số nguyên x,y biết:xy-3x-2y=11
Bài 3. Cho hình vẽ:
Biết a//b; góc A bằng 450; góc B bằng 300.
Tính số đo góc M.
Dựng tia Mz // a // b
Do Mz // a \(\Rightarrow\widehat{M_1}=\widehat{A}=45^o\)( 2 góc so le trong)
Do Mz // b \(\Rightarrow\widehat{M_2}=\widehat{B}=30^o\)
Ta thấy: \(\widehat{M}=\widehat{M_1}+\widehat{M_2}=45^o+30^o=75^o\)
Cho hai đường thẳng a và b. Đường thẳng AB cắt hai đường thẳng trên tại hai điểm A và B.
a) Hãy nêu tên những cặp góc sole trong, những cặp góc đối đỉnh, những cặp góc kề bù.
Biết \(\widehat{A_1}=100^0\), \(\widehat{B_1}=115^0\). Tính những góc còn lại.
Cho hai đường thẳng a và b .Đường thẳng AB cắt hai đường thẳng trên tại hai điểm A và B .
a/Hãy nêu tên những cặp góc so le trong,những cặp góc đối đỉnh , những cặp góc kề bù .
b/Biết \(\widehat{A_1}=100^o\),\(\widehat{B_1}=115^o.\)Tính những góc còn lại.
Em nghĩ chị nên lên học 24h để được giải đáp tốt hơn vì ở đây chắc chỉ dành cho lớp 5 trở xuống ạ !