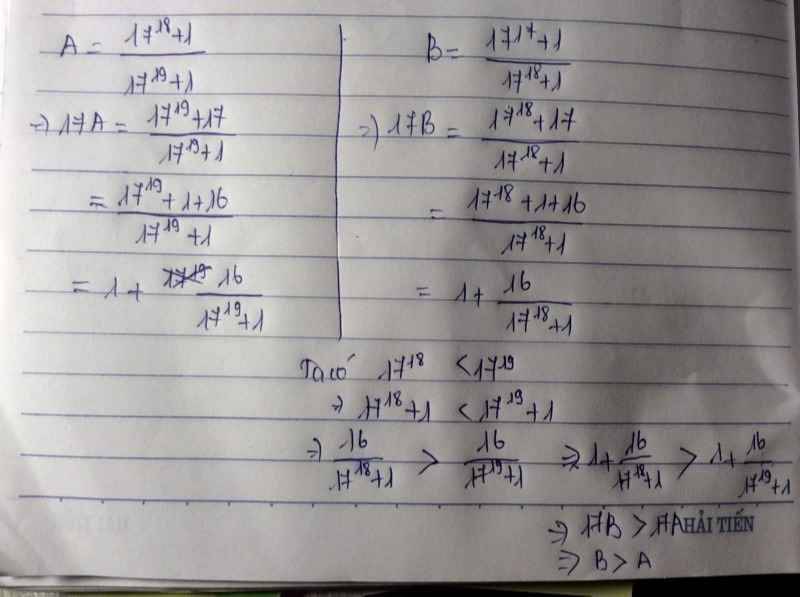17+18=
DT
Những câu hỏi liên quan
giải phương trình :
1/(16√17+17√16)+1/(17√18+18√17)+1/(18√19+19√18)+⋯+1/(x√(x+1)+(x+1)√x)=499/2012
So sánh: A=17^18+1/17^19+1 và B= 17^17+1/17^18+1
Nếu nghĩ kĩ thì thấy bài này cũng đơn giản thôi.Thử xem cách giải của mk nè:
Giải: Ta có: A=\(\frac{17^{18}+1}{17^{19}+1}\) B=\(\frac{17^{17}+1}{17^{18}+1}\)
17A=\(\frac{17^{19}+17}{17^{19}+1}\) 17B=\(\frac{17^{18}+17}{17^{18}+1}\)
17A=\(\frac{\left(17^{19}+1\right)+16}{17^{19}+1}\) 17B=\(\frac{\left(17^{18}+1\right)+16}{17^{18}+1}\)
17A=\(\frac{17^{19}+1}{17^{19}+1}+\frac{16}{17^{19}+1}\) 17B=\(\frac{17^{18}+1}{17^{18}+1}+\frac{16}{17^{18}+1}\)
17A=\(1+\frac{16}{17^{19}+1}\) 17B= \(1+\frac{16}{17^{18}+1}\)
Lại có: 1719+1>1718+1
Suy ra:\(\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
17A<17B
A<B
Vậy A<B
Đúng 1
Bình luận (0)
\(\text{Ta có:}\frac{17^{18}+1}{17^{19}+1}\)
\(\Rightarrow17A=\frac{17^{19}+1+16}{17^{19}+1}\)
\(\Rightarrow17A=1+\frac{16}{17^{19}+1}\)
\(B=\frac{17^{17}+1}{17^{18}+1}\)
\(\Rightarrow17B=\frac{17^{18}+1+16}{17^{18}+1}\)
\(\Rightarrow17B=1+\frac{16}{17^{18}+1}\)
\(\text{Vì }\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)
\(\Rightarrow17A< 17B\)
\(\Rightarrow A< B\)
Số lượng học sinh nữ mỗi lớp của một trường Trung học cơ sở được ghi nhận dưới bảng sau:
17
18
20
17
24
17
22
16
16
24
18
15
20
22
18
15
15
18
17
18
Tần số tương ứng của các giá trị 15, 17, 20, 24 A. 3, 2, 2, 1 B. 2, 4, 5, 2 C. 3, 4, 2, 2 D. 2, 5, 2, 1
Đọc tiếp
Số lượng học sinh nữ mỗi lớp của một trường Trung học cơ sở được ghi nhận dưới bảng sau:
| 17 | 18 | 20 | 17 |
| 24 | 17 | 22 | 16 |
| 16 | 24 | 18 | 15 |
| 20 | 22 | 18 | 15 |
| 15 | 18 | 17 | 18 |
Tần số tương ứng của các giá trị 15, 17, 20, 24
A. 3, 2, 2, 1
B. 2, 4, 5, 2
C. 3, 4, 2, 2
D. 2, 5, 2, 1
Tần số tương ứng của các giá trị 15, 17, 20, 24 là 3, 4, 2, 2
Chọn đáp án C.
Đúng 1
Bình luận (0)
Help meeeee. E đang cần gấp.
So sánh
A=17^18+1/17^19 và B=17^17+1/17^18+1
A=(17^18+1)/(17^19+1)
17A=17(17^18+1)/17^19+1=17^19+17/17^19+1
17A=(17^19+1)+16/(17^19+1)=1+16/17^19+1
B=(17^17+1)/(17^18+1)
17B=17(17^17+1)/17^18+1=17^18+17/17^18+1
17B=(17^18+1)+16/(17^18+1)=1+16/17^18+1
Từ (1) và (2)⇒1+16/17^19+1<1+16/17^18+1
=> 17A<17B
Hay A<B
Vậy A<B
Đúng 0
Bình luận (0)
[1/18+2/17+.......18/1+18] : [1/18+1/17+...+1/1]
Đặt A = \(\frac{\frac{1}{18}+\frac{2}{17}+....+\frac{18}{1}+18}{\frac{1}{18}+\frac{1}{17}+....+\frac{1}{1}}\)
Xét TS (tử số) của A ta có:
TS = \(\frac{1}{18}+\frac{2}{17}+...+\frac{18}{1}+18\)
\(TS=\left(\frac{1}{18}+1\right)+\left(\frac{2}{17}+1\right)+...+\left(\frac{18}{1}+1\right)\) (chia 18 ra 18 phần 1 đơn vị cộng lại cho mỗi phân số)
\(TS=\frac{19}{18}+\frac{19}{17}+...+\frac{19}{1}=19.\left(\frac{1}{18}+\frac{1}{17}+...+\frac{1}{1}\right)\)
Thay lại TS vào A ta có:
\(A=\frac{19.\left(\frac{1}{18}+\frac{1}{17}+...+\frac{1}{1}\right)}{\left(\frac{1}{18}+\frac{1}{17}+...+\frac{1}{1}\right)}=19\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh : A= 17^18 + 1 / 17^19+1
Và B =17^17+1 / 17^18+1
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}\)
\(=\frac{17^{18}+17}{17^{19}+17}\)
\(=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}\)
\(\Leftrightarrow\frac{17^{17}+1}{17^{18}+1}\)'
\(\Rightarrow=B\)
Vậy \(A< B\)
Đúng 0
Bình luận (0)
So sánh A và B biết:
A=\(\dfrac{17^{18}+1}{17^{19}+1}\) , B=\(\dfrac{17^{17}+1}{17^{18}+1}\)
\(17A=\dfrac{17^{19}+17}{17^{19}+1}=\dfrac{\left(17^{19}+1\right)+16}{17^{19}+1}=\dfrac{17^{19}+1}{17^{19}+1}+\dfrac{16}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}=\dfrac{\left(17^{18}+1\right)+16}{17^{18}+1}=\dfrac{17^{18}+1}{17^{18}+1}+\dfrac{16}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)
Vì \(17^{19}>17^{18}=>17^{19}+1>17^{18}+1\)
\(=>\dfrac{16}{17^{19}+1}< \dfrac{16}{17^{18}+1}\)
\(=>17A< 17B=>A< B\)
Đúng 1
Bình luận (0)
So sánh C và D:
C=17^18-2/17^17-2 và 17^19-2/17^18-2
Ta có : \(17^{17}-2< 17^{18}-2\)
Mà mẫu số càng lớn thì p/s càng bé
\(\Rightarrow\)\(\frac{2}{17^{17}-2}< \frac{2}{17^{18}-2}\)
Lại có :\(17^{18}< 17^{19}\)
\(\Rightarrow\)\(17^{18}-\frac{2}{17^{17}-2}< 17^{19}-\frac{2}{17^{18}-2}\)\(17^{18}-\frac{2}{17^{17}-2}< 17^{19}-\frac{2}{17^{18}-2}\)\(17^{18}-\frac{2}{17^{17}-2}< 17^{19}-\frac{2}{17^{18}-2}\)\(17^{18}-\frac{2}{17^{17}-2}< 17^{19}-\frac{2}{17^{18}-2}\)\(17^{18}-\frac{2}{17^{17}-2}< 17^{19}-\frac{2}{17^{18}-2}\)( Vì số bị trừ càng lớn thì hiệu càng bé )
Đúng 0
Bình luận (0)
cho S=17 + 17^2 + 17^3+........+17^18
Tìm ƯCLN của 18 và S
Số lượng học sinh nữ mỗi lớp của một trường Trung học cơ sở được ghi nhận dưới bảng sau:
17
18
20
17
24
17
22
16
16
24
18
15
20
22
18
15
15
18
17
18
Có bao nhiêu giá trị khác nhau của dấu hiệu A. 7 giá trị B. 9 giá trị C. 14 giá trị D. 20 giá trị
Đọc tiếp
Số lượng học sinh nữ mỗi lớp của một trường Trung học cơ sở được ghi nhận dưới bảng sau:
| 17 | 18 | 20 | 17 |
| 24 | 17 | 22 | 16 |
| 16 | 24 | 18 | 15 |
| 20 | 22 | 18 | 15 |
| 15 | 18 | 17 | 18 |
Có bao nhiêu giá trị khác nhau của dấu hiệu
A. 7 giá trị
B. 9 giá trị
C. 14 giá trị
D. 20 giá trị
Có 7 giá trị khác nhau của dấu hiệu là: 15, 16, 17, 18, 20, 22, 24
Chọn đáp án A.
Đúng 0
Bình luận (0)