Tìm GTLN,GTNN của \(P=\dfrac{x^2+xy-y^2}{x^2-2xy+4y^2}\)
H24
Những câu hỏi liên quan
Tìm GTLN hoặc GTNN của các đa thức sau
B=-x^2 + 2xy - 4y^2 +2x +10y -9
D=2(x+y) +xy -x^2 - y^2
1. Cho x,y,z0, x+yle1 và xyz1. Tìm GTLN của biểu thức Pdfrac{1}{1+4x^2}+dfrac{1}{1+4y^2}-sqrt{z+1}
2. Cho x,y,z0, xyzx+y+z. Tìm GTNN của biểu thức Pxy+yz+zx-sqrt{1+x^2}-sqrt{1+y^2}-sqrt{1+z^2} (dùng phương pháp lượng giác hóa)
Đọc tiếp
1. Cho \(x,y,z>0\), \(x+y\le1\) và \(xyz=1\). Tìm GTLN của biểu thức \(P=\dfrac{1}{1+4x^2}+\dfrac{1}{1+4y^2}-\sqrt{z+1}\)
2. Cho \(x,y,z>0\), \(xyz=x+y+z\). Tìm GTNN của biểu thức \(P=xy+yz+zx-\sqrt{1+x^2}-\sqrt{1+y^2}-\sqrt{1+z^2}\) (dùng phương pháp lượng giác hóa)
f(x)(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNNF2x^2+3y^2-8x+24y-7 tìm GTNNF-5x^2-4y^2+20x-32y+9 tìm GTLNFx^2+y^2-x+y-3 tìm GTNNFF5x^2+y^2-4xy-6x+20 tìm GTNNF-13x^2-4y^2+12xy+20x+37F5x^2+9y^2-12xy+24x-48y+100Cho x+y5 Cho A x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của ACho x+y+20 Tìm min của B2(x^3+y^3)-15xy+7Cho x+y+20 tìm min của Cx^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy
Đọc tiếp
f(x)=(2x-3)^2+(x+4)^2-(3x^2+5x-2) tìm GTNN
F=2x^2+3y^2-8x+24y-7 tìm GTNN
F=-5x^2-4y^2+20x-32y+9 tìm GTLN
F=x^2+y^2-x+y-3 tìm GTNN
F=F=5x^2+y^2-4xy-6x+20 tìm GTNN
F=-13x^2-4y^2+12xy+20x+37
F=5x^2+9y^2-12xy+24x-48y+100
Cho x+y=5 Cho A= x^3+y^3-8(x^2+y^2)+xy+2 tính GTLN của A
Cho x+y+2=0 Tìm min của B=2(x^3+y^3)-15xy+7
Cho x+y+2=0 tìm min của C=x^4+y^4-(x^3+y^3)+2x^2y^2+2xy(x^2+y^2)+13xy
bài 1 : tìm x,y sao cho :
A=2x^2 +9y^2-6xy-6x-12y+2014 đạt gtnn ?
B= -x^2+2xy-4y^2+2x+10y-8 đạt gtln ?
bài 2 : tìm các số nguyên x,y không nhỏ hơn 2 soa cho xy-1 chia hết cho (x-1)(y-1)
kí hiệu a l b là a chia hết cho b nhé
xy-1 l (x-1)(y-1) <=> xy-1 l y-1 <=> y(x-1)+y-1 l y-1 => x-1 l y-1
tương tự : y-1 l x-1
=> \(\orbr{\begin{cases}x-1=y-1\\x-1=1-y\end{cases}}\Rightarrow\orbr{\begin{cases}x=y\\x+y=2\end{cases}}\)
+> x=y \(\Rightarrow x^2-1\)l \(\left(x-1\right)^2\) <=> x+1 l x-1 <=> 2 l x-1 => x=2 hoặc x=3
|+> x+y=2 thay vào tương tự như trên nhé
Đúng 0
Bình luận (0)
cho x,y thỏa mản \(x^2+2xy+4y+3y^2+3=0\)
tìm gtln ; gtnn của b=x+y+z
\(x^2+2xy+4y+3y^2+3=0\)0
=>\(\left(x^2+2xy+y^2\right)\)+\(\left(2y^2+4y+2\right)+1\)=0
=>(x+y)2+2(y+1)2+1=0 (vo li)
=> đề sai khỏi làm
Đúng 0
Bình luận (0)
Bài 1: Tìm min max
x^2 +2xy +7(x+y) +2y^2 +10 = 0
Bài 2 : cho x, y không âm thỏa mãn x+y = 4 tìm GTNN GTLN
p= x^4y+xy^4+x^3+y^3-5(x^2 + y ^2 + 14x^2y^2 -58xy +6
--------- Giúp nha !
Cho x,y,z là các số thực dương thỏa mãn: x^2+y^2+z^2=2.Tìm GTNN và GTLN của P=\(\dfrac{x}{2+yz}+\dfrac{y}{2+zx}+\dfrac{z}{2+xy}\)
Ta thấy
72
=
2
3
.
3
2
72=2
3
.3
2
nên a, b có dạng
{
�
=
2
�
3
�
�
=
2
�
.
3
�
{
a=2
x
3
y
b=2
z
.3
t
với
�
,
�
,
�
,
�
∈
N
x,y,z,t∈N và
�
�
�
{
�
,
�
}
=
3
;
�
�
�
{
�
,
�
}
=
2
max{x,z}=3;max{y,t}=2.
Theo đề bài, ta có
2
�
.
3
�
+
2
�
.
3
�
=
42
2
x
.3
y
+2
z
.3
t
=42
⇔
2
�
−
1
.
3
�
−
1
+
2
�
−
1
3
�
−
1
=
7
⇔2
x−1
.3
y−1
+2
z−1
3
t−1
=7 (*), do đó
�
,
�
,
�
,
�
≥
1
x,y,z,t≥1
TH1:
�
≥
�
,
�
≤
�
x≥z,y≤t. Khi đó
�
=
3
,
�
=
2
x=3,t=2. (*) thành:
4.
3
�
−
1
+
3.
2
�
−
1
=
7
4.3
y−1
+3.2
z−1
=7
⇔
�
=
�
=
1
⇔y=z=1
Vậy
{
�
=
24
�
=
18
{
a=24
b=18
(nhận)
TH2: KMTQ thì giả sử
�
≥
�
,
�
≥
�
x≥z,y≥t. Khi đó
�
=
3
,
�
=
2
x=3,z=2. (*) thành
4.
3
�
−
1
+
2.
3
�
−
1
=
7
4.3
y−1
+2.3
t−1
=7, điều này là vô lí.
Vậy
(
�
,
�
)
=
(
24
,
18
)
(a,b)=(24,18) hay
(
18
,
24
)
(18,24) là cặp số duy nhất thỏa yêu cầu bài toán.
Đúng 0
Bình luận (0)
Tìm GTLN và GTNN của P=2x2-xy-y2 với x,y thỏa mãn x2+2xy+3y2=4
B1: cho x-2y=2. tìm GTNN của Q= \(x^2+2y^2-x+3y\)
B2: a) tìm GTLN của P=\(x^2+y^2+xy+x+y\)
b) tìm GTLN của Q=\(-5x^2-2xy-2y^2+14x+10y-1\)
Bài 2 :
a) \(P=x^2+y^2+xy+x+y\)
\(2P=2x^2+2y^2+2xy+2x+2y\)
\(2P=x^2+2xy+y^2+x^2+2x+1+y^2+2y+1-2\)
\(2P=\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2-2\)
\(P=\frac{\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2-2}{2}\)
\(P=\frac{\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-1\le-1\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+1=0\\y+1=0\end{cases}}\)
Mình nghĩ đề phải là tìm GTLN của \(P=x^2+y^2+xy+x-y\)hoặc đổi dấu x và y thì dấu "=" mới xảy ra đc
Đúng 0
Bình luận (0)
@ Phương ơi ! Cái dòng \(P=\)cuối ấy . Chỗ đấy là \(\ge-1\)em nhé!
Đúng 0
Bình luận (0)
a,Cho x,y,z tm \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\x+y+z=4\end{matrix}\right.\). CM: \(-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b, cho \(x^2+3y^2=1\). Tìm GTLN, GTNN của\(P=x-y\)
c, Cho \(P=\dfrac{x^2-\left(x-4y\right)^2}{x^2+4y^2}\left(x^2+y^2>0\right)\)
Tìm GTLN của P
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Đúng 3
Bình luận (2)
Bài a hình như sai đề rồi bạn.
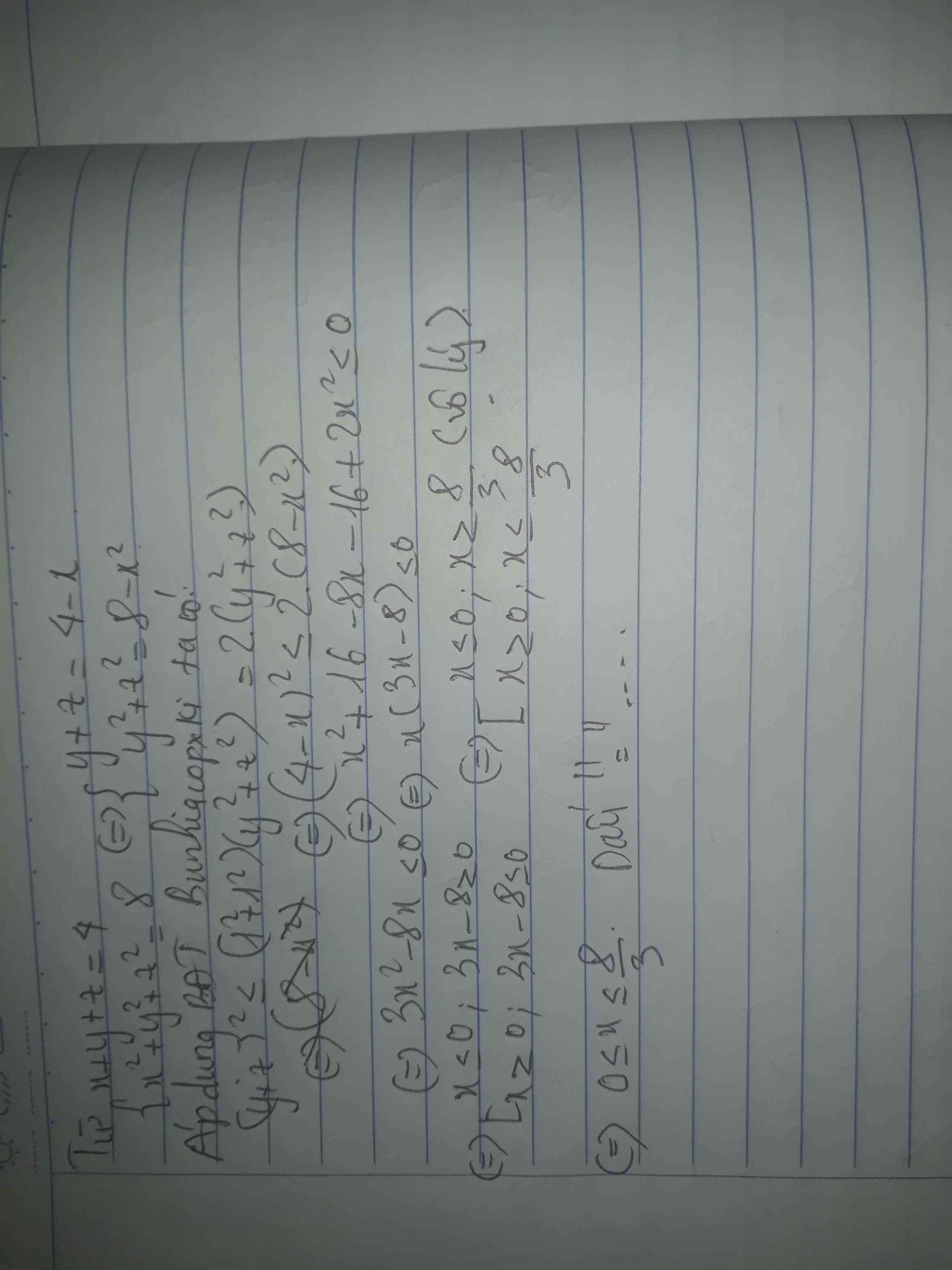
Đúng 3
Bình luận (2)
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời






