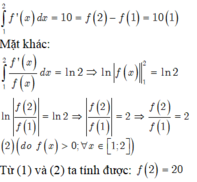cho hàm số f(x) thỏa mãn f(f(x)) = x + 10. Biết f(2001) = 2001. Tính f(2011)
DT
Những câu hỏi liên quan
Cho hàm số f(x) thỏa mãn f(f(x)) = x + 10. Biết f(2001) = 2011. Tính f(2011)
\(f\left(2011\right)=f\left(f\left(2001\right)\right)=2001+10=2011\)
Vậy \(f\left(2011\right)=2011\)
Cho hàm số f(x) thỏa mãn f(f(x))=x+10. Biết f(2001)=2011. Tính f(2011)
có ai ko giúp mình với :))
hình như sai đề bài rồi bạn ơi
f(f(x)????
sửa lại đi mình làm cho
chúc bạn học tốt
>.<
Đúng 0
Bình luận (0)
a.Tìm các cặp số x,y thoả mãn\(|x^4-1|+|y^2-3|=0\)
b.Cho hàm số f(x) thoả mãn f(f(x))=x+10, biết f(2001)=2011
a, \(\left|x^4-1\right|\)\(+\left|y^2-3\right|=0\)
-Vì: $\left\{\begin{matrix}
|x^4-1|\geq 0 & \\
|y^2-3|\geq 0 &
\end{matrix}\right.$
-Để: $|x^4-1|+|y^2-3|=0$
-Thì:
$\Rightarrow \left\{\begin{matrix}
|x^4-1|=0 & \\
|y^2-3|=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4-1=0 & \\
y^2-3=0 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x^4=1 & \\
y^2=3 &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=\pm 1 & \\
y=\pm \sqrt{3} &
\end{matrix}\right.$
b, Đề thiếu kìa bạn!!
Đúng 0
Bình luận (0)
Cho f(x) bậc 3 với hệ số của x3 là : k ( k thuộc Z ) thỏa mãn :
f(1999) = 2000 ; f(2000) = 2001
tính f(2001) - f(1998)
Cho hàm số y f(x) có đạo hàm liên tục trên [1;2] thỏa mãn
∫
1
2
f
(
x
)
d
x
10
và
∫
1
2
f
(
x
)
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên [1;2] thỏa mãn ∫ 1 2 f ' ( x ) d x = 10 và ∫ 1 2 f ' ( x ) f ( x ) d x = ln 2 . Biết rằng f(x)>0. Tính f(2)
A. f(2) = 10
B. f(2) = -20
C. f(2) = -10
D. f(2) = 20
cho hàm số y=f(x) thỏa mãn: f(x) + 3.f(2x)= x+1. Tính f(10)
cho đa thức f(x) bậc 3 với hệ số \(x^3\)là số nguyên thỏa mãn \(f\left(1999\right)=2000;f\left(2000\right)=2001\). Chứng minh \(f\left(2001\right)-f\left(1998\right)\)là hợp số
Cho hàm số y=f(x) thỏa mãn f(x+y)=f(x).f(y) . Biết f(2019)=2020. tính f(2020)
Ta có:\(f\left(x\right).f\left(y\right)=f\left(x.y\right)\)
\(\Rightarrow f\left(x+y\right)=f\left(x.y\right)\)
\(\Rightarrow f\left(2019\right)=f\left(0+2019\right)=f\left(0.2019\right)=f\left(0\right)=2020\)
\(\Rightarrow f\left(2020\right)=f\left(0+2020\right)=f\left(0.2020\right)=f\left(0\right)\)
\(\Rightarrow f\left(2019\right)=f\left(2020\right)=f\left(0\right)=2020\)
Đúng 0
Bình luận (0)
khó quá.
Tại sao : \(f\left(0+2019\right)=f\left(0.2019\right)\)? logic, hay do mk ngu ... 2019 = 0 à ?
Cho hàm số f(x) có đạo hàm f(x) thỏa mãn các đẳng thức
∫
0
1
(
2
x
-
1
)
f
(
x
)
d
x
10
,
...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) thỏa mãn các đẳng thức ∫ 0 1 ( 2 x - 1 ) f ' ( x ) d x = 10 , f ( 1 ) + f ( 8 ) = 0 . Tính I = ∫ 0 1 f ( x ) d x .
A. I = 2.
B. I = 1.
C. I = -1.
D. I = -2.