CM số hoán vị của 123...n = n!
MC
Những câu hỏi liên quan
Bạn có một hoán vị: một mảng a [a1, a2,…, an] gồm các số nguyên phân biệt từ 1 đến n. Độ dài của hoán vị n là số lẻ. Hãy xem xét thuật toán sắp xếp hoán vị theo thứ tự tăng dần sau đây. Thủ tục trợ giúp của thuật toán, f (i) , nhận một đối số duy nhất i (1≤i≤n − 1) và thực hiện như sau. Nếu ai ai + 1, giá trị của ai và ai + 1 được trao đổi. Nếu không, hoán vị không thay đổi. Thuật toán bao gồm các lần lặp, được đánh số bằng các số nguyên liên tiếp bắt đầu bằng 1 . Trên tôi -lặp lại thứ, thuật t...
Đọc tiếp
Bạn có một hoán vị: một mảng a = [a1, a2,…, an] gồm các số nguyên phân biệt từ 1 đến n. Độ dài của hoán vị n là số lẻ. Hãy xem xét thuật toán sắp xếp hoán vị theo thứ tự tăng dần sau đây. Thủ tục trợ giúp của thuật toán, f (i) , nhận một đối số duy nhất i (1≤i≤n − 1) và thực hiện như sau. Nếu ai> ai + 1, giá trị của ai và ai + 1 được trao đổi. Nếu không, hoán vị không thay đổi. Thuật toán bao gồm các lần lặp, được đánh số bằng các số nguyên liên tiếp bắt đầu bằng 1 . Trên tôi -lặp lại thứ, thuật toán thực hiện như sau:
nếu tôi là số lẻ, gọi f (1), f (3),…, f (n − 2) ;
nếu tôi là chẵn, gọi f (2), f (4),…, f (n − 1) .
Có thể chứng minh rằng sau một số lần lặp lại hữu hạn, hoán vị sẽ được sắp xếp theo thứ tự tăng dần. Sau bao nhiêu lần lặp lại điều này sẽ xảy ra lần đầu tiên?
Input:
Đầu vào Mỗi thử nghiệm chứa nhiều trường hợp thử nghiệm. Dòng đầu tiên chứa số lượng trường hợp thử nghiệm t (1≤t≤10 ^ 4 ). Sau đây là mô tả các trường hợp kiểm thử. Dòng đầu tiên của mỗi trường hợp kiểm tra chứa một số nguyên n (3≤n≤2⋅10 ^ 5−1; n là lẻ) - độ dài của hoán vị. Dòng thứ hai chứa n các số nguyên phân biệt a1, a2,…, an (1≤ai≤n ) - hoán vị chính nó. Đảm bảo rằng tổng của n trên tất cả các trường hợp thử nghiệm không vượt quá 2⋅10 ^ 5−1
Output:
. Đầu ra Đối với mỗi trường hợp thử nghiệm, in số lần lặp lại mà sau đó hoán vị sẽ được sắp xếp theo thứ tự tăng dần lần đầu tiên. Nếu hoán vị đã cho đã được sắp xếp, hãy in ra 0.
Input:
3
3
3 2 1
7
4 5 7 1 3 2 6
5
1 2 3 4 5
ouput:
3
5
0
Ghi chú Trong trường hợp thử nghiệm đầu tiên, hoán vị sẽ thay đổi như sau: sau 1 lần lặp -st: [2,3,1] ; sau 2 -nd lần lặp: [2,1,3] ; sau 3 -lặp lại thứ ba: [1,2,3] . Trong trường hợp thử nghiệm thứ hai, hoán vị sẽ thay đổi như sau: sau 1 lần lặp -st: [4,5,1,7,2,3,6] ; sau 2 -nd lần lặp: [4,1,5,2,7,3,6] ; sau 3 -lặp lại thứ ba: [1,4,2,5,3,7,6] ; sau 4 -lần lặp thứ: [1,2,4,3,5,6,7] ; sau 5 -lặp lại thứ: [1,2,3,4,5,6,7] . Trong trường hợp thử nghiệm thứ ba, hoán vị đã được sắp xếp và câu trả lời là 0 .
gốc: https://codeforces.com/problemset/problem/1558/F
Đúng 0
Bình luận (0)
Cho tập hợp X có n phần tử n ∈ N * , số hoán vị n phần tử của tập hợp X là
A.n!
B.n
C. n 2
D. n 3
Cho tập hợp X có n phần tử
n
∈
N
*
, số hoán vị n phần tử của tập hợp X là A. n! B. n C.
n
2
D.
n
3
Đọc tiếp
Cho tập hợp X có n phần tử n ∈ N * , số hoán vị n phần tử của tập hợp X là
A. n!
B. n
C. n 2
D. n 3
Viết công thức tính số hoán vị của tập hợp gồm n phần tử n > 1 . Nêu ví dụ.
+ Cho tập A gồm n phần tử.
Mỗi hoán vị của A là kết quả của sự sắp xếp thứ tự n phần tử của tập A.
+ Số các hoán vị: Pn = n! = 1.2.3.4.5….n.
Ví dụ: Số hoán vị của tập gồm 6 phần tử là: P6 = 6! = 720.
Số hoán vị của tập gồm 3 phần tử là: P3 = 6.
Đúng 0
Bình luận (0)
Cho hoán vị s của tập {1,2,3,4,5} xác định bởi s(1)=1, s(2)=5, s(3)=3, s(4)=2, s(5)=4. Hỏi s là chẵn hay lẻ? Hãy tìm số tự nhiên n nhỏ nhất để hợp thành n lần của s thì được hoán vị đồng nhất.
Tìm số nguyên dương n thỏa mãn
1
+
P
1
+
2
P
3
+
3
P
3
+
.
.
.
+
n
P
n
P
2014
, với
P
n
là số các hoán vị của tập hợp có n phần tử. A. 2013 B. 2014 C. 2015 D. 2016
Đọc tiếp
Tìm số nguyên dương n thỏa mãn 1 + P 1 + 2 P 3 + 3 P 3 + . . . + n P n = P 2014 , với P n là số các hoán vị của tập hợp có n phần tử.
A. 2013
B. 2014
C. 2015
D. 2016
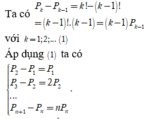
Cộng các đẳng thức ở (2) ta được ![]()
Do
P
1
=
1
![]()
Theo đề, ta có ![]()
Chọn A.
Đúng 0
Bình luận (0)
viết chương trình pascal Hoán vị ký tự theo khóa - Tên chương trình GRCAE.???
Nhập vào xâu S chỉ chứa các ký tự là chỉ cái in thường và khoảng trắng.
Cho trước khóa m là một hoán vị của n số (2n18). Để mã hóa một xâu ký tự ta có thể chia xâu thành từng nhóm từ trái sang phải mỗi nhóm có n ký tự; nếu nhóm cuối không đủ n ký tự thì ta có thể thêm các ký tự trắng vào sau cho đủ. Sau đó hoán vị các ký tự trong từng nhóm theo khóa, ghép các nhóm xâu lại theo thứ tự ta được một xâu đã mã hóa. Hãy vi...
Đọc tiếp
viết chương trình pascal Hoán vị ký tự theo khóa - Tên chương trình GRCAE.???
Nhập vào xâu S chỉ chứa các ký tự là chỉ cái in thường và khoảng trắng.
Cho trước khóa m là một hoán vị của n số (2<n<18). Để mã hóa một xâu ký tự ta có thể chia xâu thành từng nhóm từ trái sang phải mỗi nhóm có n ký tự; nếu nhóm cuối không đủ n ký tự thì ta có thể thêm các ký tự trắng vào sau cho đủ. Sau đó hoán vị các ký tự trong từng nhóm theo khóa, ghép các nhóm xâu lại theo thứ tự ta được một xâu đã mã hóa. Hãy viết chương trình mã hóa một xâu kí tự cho trước.
Ví dụ: Với n=8 và khóa m=87345621, thực mã hóa xâu S = “hello every body” như sau:
Tách xâu S thành các xâu mỗi xâu có 8 ký tự:
S1 = “hello ev”; S2 = “ery o body”
Thực hiện mã hóa xâu S1, S2 theo khóa m ta được S1’ và S2’:
S1’ = “vello eh”; S2’ =”ydy bore”
Input: GRCAE.INP
· Dòng 1: số nguyên n (2<n<18) và m (m là số nguyên có n chữ số).
· Dòng 2: ghi xâu cần mã hóa (độ dài xâu <=10^5).
Ouput: GRCAE.OUT
· Mỗi dòng ghi 1 xâu có n ký tự đã được mã hóa.
Ví dụ:
GRCAE.INP GRCAE.OUT
8 87345621
hello every body vello eh ydy bore
Tính số hoán vị của n phần tử :
\(P_n=A^n_n=n\left(n-1\right)\left(n-2\right)...2.1=n!\)
( n! : n giai thừa )
Tìm số hoán vị của n phần tử trong đó có 2 phần tử a và b không đứng cạnh nhau.
A. (n-1)n!
B. (n-1)!
C. (n-2)(n-1)!
D. n!-2