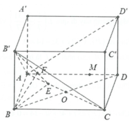
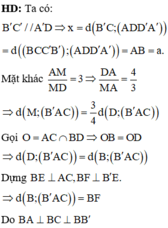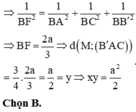Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AB = a√3, B A D ^ = 120 o . Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30 o . Gọi M là trung điểm A'D', N là trung điểm BB'. Tính khoảng cách từ N đến mặt phẳng (C'MA)
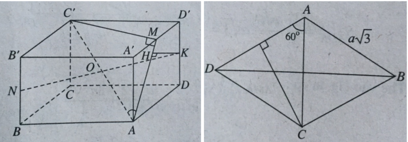
Nhận xét:
Do tam giác A’B’D’ là tam giác đều nên C’M ⊥ A’D’
(C'A'D') ⊥ (AA'D'D) & (C'A'D') ∩(AA'D'D) ⇒ C’M ⊥ (AA’D’D)
Nên ∠(AC',(AA'D'D)) = ∠(C'AM) = 30 o .
Gọi K là trung điểm của DD’, ta có AKC’N là hình bình hành nên K với N đối xứng nhau qua trung điểm O của AC’. Mà O ∈ (AMC’), do đó
d[N,(C'MA)] = d[K,(C'MA)]
+ Xác định khoảng cách từ K đến (C’MA).
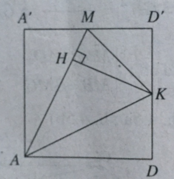
Do (C’MA) vuông góc với (AA’D’D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có KH ⊥ (C’MA) hay d[K,(C'MA)] = KH.
+ Tính KH.
Ta có: SAMK = SAA'D'D – (SAA'M + SMD'K + SADK) (1)
Trong tam giác AMC’, ta có: A M = C ’ M . c o t 30 o = ( 3 a √ 3 ) / 2 .
Trong tam giác AA’M, ta có: A A ’ = A M 2 - A ' M 2 = a √ 6 .

Đúng 0
Bình luận (0)
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.ABCD cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và AD bằng A.
a
2
2
B. a. C.
a
2
D.
a
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và A'D' bằng
A. a 2 2
B. a.
C. a 2
D. a 3
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và A'D' bằng
A. a 2 2
B. a
C. a 2
D. a 3
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 . Tính khoảng cách d từ điểm A đến mp (BDA')
Giải chi tiết:

Dễ thấy, tứ diện A.A′BD�.�′�� có ba cạnh AB,AD,AA′��,��,��′ đôi một vuông góc.
Đặt d=d(A,(A′BD))�=�(�,(�′��)) ta có :
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD có độ dài cạnh bằng 10. Tính khoảng cách giữa hai mặt phẳng
A
D
D
A
và
B
C
C
B
A.
10
B. 100 C. 10 D. 5
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh bằng 10. Tính khoảng cách giữa hai mặt phẳng A D D ' A ' và B C C ' B '
A. 10
B. 100
C. 10
D. 5
Cho hình lập phương ABCD.ABCD cạnh bằng a. Gọi K là trung điểm DD. Tính khoảng cách giữa hai đường thẳng CK và AD. A. 4a/3 B. a/3 C. 2a/3 D. 3a/4
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. 4a/3
B. a/3
C. 2a/3
D. 3a/4
Chọn B
Gọi M là trung điểm BB'. Ta có: CK // A'M => CK // (A'MD)
Khi đó d(CK, A'D) = d (CK, (A'MD)). Gắn hệ trục tọa độ như hình vẽ:
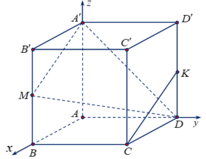
Ta có: A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a), B'(a;0;a), C(a;a;0), M(a;0;a/2).
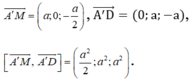
Vậy mặt phẳng (A'MD) nhận ![]() làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
Phương trình (A'MD) là x + 2y + 2z - 2a = 0
Do đó: 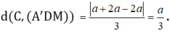
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a. Gọi K là trung điểm của DD. Khoảng cách giữa hai đường thẳng CK và AD bằng A.
a
3
B.
a
2
C.
a
6
D.
a
3
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi K là trung điểm của DD'. Khoảng cách giữa hai đường thẳng CK và A'D bằng
A. a 3
B. a 2
C. a 6
D. a 3
Chọn D.

Phương pháp: Phương pháp tọa độ.
Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1


Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AA và BC bằng:
A
.
a
3
B
.
a
3
2
C
.
a
D
.
a
3
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AA' và B'C bằng:
A . a 3
B . a 3 2
C . a
D . a 3 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
A
a
. Gọi M là điểm trên đoạn AD với
A
M
M
D...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A A ' = a . Gọi M là điểm trên đoạn AD với A M M D = 3 . Gọi x là độ dài khoảng cách giữa hai đường thẳng A'D, B'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB'C). Tính giá trị xy.
A. 5 a 2 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2