b+b/bxb = 1/2
a+a=b
bxb=d
b+b=d
cxcxaxa=c
axa=a
gọi a,b,c là 3 cạnh của tam giác bất kì CMR:
2x(axb+bxc+cxa)>axa+bxb+cxc
Cho hàm số y = x 3 − 3 x + 1 có đồ thị (C) Gọi A x A ; y A , B x B , y B với x A > x B là các điểm thuộc (C) sao cho các tiếp tuyến tại A,B song song với nhau và A B = 6 37 . tính S = 2 x A − 3 x B
A. S=90
B. S=-45
C. S=15
D. S=-9
Đáp án là C.
y ' = 3 x 2 − 3 ;
y ' x A = 3 x A 2 − 3 ;
y ' x B = 3 x B 2 − 3
Tiếp tuyến tại A,B song song nên y ' x A = y ' x B ⇔ 3 x A 2 − 3 = 3 x B 2 − 3
⇔ x A = x B lo¹i do x A > x B x A = − x B chän
Ta có :
A B 2 = x B − x A 2 + y B − y A 2 = x B − x A 2 + x B 3 − 3 x B + 1 − x A 3 − 3 x A + 1 2
= 4 x B 6 − 24 x B 4 + 40 x B 2
Giả thiết A B = 6 37
⇔ 4 x B 6 − 24 x B 4 + 40 x B 2 = 36.37 ⇔ x B 2 3 − 6 x B 2 2 + 10 x B 2 − 333 = 0
⇔ x B 2 = 9 ⇔ x B = 3 ⇒ x A = − 3 lo¹i x B = − 3 ⇒ x A = 3 chän
Vậy S = 2 x A − 3 x B = 2.3 − 3 − 3 = 15 .
kết quả của biểu thức (36-a:a)x(9:bxb=c:c)
A.3249 B.3600 C.3610 D.KHÔNG TÍNH ĐƯỢC
Đường thẳng Δ có phương trình y = 2 x + 1 cắt đồ thị của hàm số y = x 3 − x + 3 tại hai điểm A và B với tọa độ được kí hiệu lần lượt là A x A ; y A và B x B ; y B trong đó x B < x A . Tìm x B + y B ?
A. x B + y B = − 5
B. x B + y B = 4
C. x B + y B = − 2
Đáp án A
Hoành độ giao điểm của đường thẳng Δ có phương trình y = 2 x + 1 và đồ thị của hàm số y = x 3 − x + 3 là nghiệm PT:
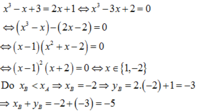
Kết quả của biểu thức (361-a:a)x(9:bxb+c:c)
A.3249 B.3600 C.3610 D.không tính được
Kết quả của biểu thức (361-a:a)x(9:bxb+c:c)
A.3249
B.3600
C.3610
D.không tính được
a:a bằng 1 nhé
Biết A x A ; y B , B x B ; y B là 2 điểm thuộc hai nhánh khác nhau của đồ thị hàm số y = x + 1 x - 1 sao cho đoạn thẳng AB có đồ dài nhỏ nhất. Tính P = x A 2 + x B 2 + y A . y B
A. P = 5 + 2
B. P = 6 + 2
C. P = 6
D. P = 5
Đường thẳng y = m tiếp xúc với đồ thị C : y = − 2 x 4 + 4 x 2 − 1 tại hai điểm phân biệt A x A ; y A v à B x B ; y B . Giá trị của biểu thức y A + y B .
A. 2
B. -1
C. 1
D. 0
Phương pháp:
Nhận xét tính chất của đường thẳng y = m dựa vào điều kiện tiếp xúc với đồ thị hàm số tại hai điểm phân biệt.
Cách giải:
Đồ thị hàm số (C) có dạng:
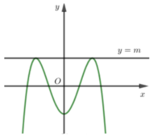
Quan sát dáng đồ thị ta thấy, nếu đường thẳng y = m tiếp xúc với đồ thị hàm số (C) tại hai điểm phân biệt thì chúng phải là hai điểm cực đại của đồ thị hàm số.
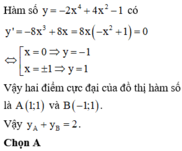
Đường thẳng Δ : y = 2 x + 1 cắt đồ thị (C) của hàm số y = x 3 − x + 3 tại hai điểm A x A ; y A và B x B ; y B , trong đó x A > x B . Tìm x B + y B
A. x B + y B = − 2
B. x B + y B = 4
C. x B + y B = 7
D. x B + y B = − 5