\(\frac{-1}{3}< \frac{x}{36}< \frac{y}{18}< \frac{-1}{4}\)
PT
Những câu hỏi liên quan
\(\frac{-1}{3}< \frac{x}{36}< \frac{y}{18}< \frac{-1}{4}\)Tìm các số x,y thòa mãn
ta có :\(\frac{-1}{3}< \frac{x}{36}< \frac{y}{18}< \frac{-1}{4}\)
=\(\frac{-12}{36}< \frac{x}{36}< \frac{y.2}{36}< \frac{-9}{36}\)
=\(\frac{-12}{36}< \frac{-11}{36}< \frac{-10}{36}< \frac{-9}{36}\)
nếu \(\frac{y.2}{36}=\frac{-10}{36}\)
thì : -10 : 2 = -5
=>\(\frac{-1}{3}< \frac{-11}{36}< \frac{-5}{36}< \frac{-1}{4}\)
Đúng 0
Bình luận (0)
1. Tìm các số nguyên x sao cho: \(\frac{-7}{12}< \frac{x-1}{4}< \frac{2}{3}\)
2. Tìm các số nguyên x,y thoả mãn:
a) \(\frac{-1}{3}< \frac{x}{36}< \frac{y}{18}< \frac{-1}{4}\)
b)\(\frac{1}{220}< \frac{x}{165}< \frac{y}{132}< \frac{1}{60}\)
1. \(\frac{-7}{12}\)< \(\frac{x-1}{4}\)< \(\frac{2}{3}\)
=> \(\frac{-7}{12}\)< \(\frac{3.\left(x-1\right)}{12}\)< \(\frac{8}{12}\)
=> 3 . ( x - 1 ) thuộc { - 6 ; - 5 ; - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7}
Lập bảng tính giá trị x , cái này dễ lên bạn tự làm nha
Đúng 0
Bình luận (0)
1/ \(-\frac{7}{12}< \frac{x-1}{4}< \frac{2}{3}\)
hay \(\frac{-7}{12}< \frac{3.\left(x-1\right)}{12}< \frac{8}{12}\)
Vậy \(-7< 3.\left(x-1\right)< 8\)
Vậy \(3.\left(x-1\right)\in\left\{-6;-5;-4;...;7\right\}\)
mà \(x\in Z\)nên \(3.\left(x-1\right)⋮3\)
Vậy \(3.\left(x-1\right)\in\left\{-6;-3;0;3;6\right\}\)
hay \(x-1\in\left\{-2;-1;0;1;2\right\}\)
tới đây dễ rồi thì làm nốt nhé, để thời gian làm mấy câu sau!
Đúng 0
Bình luận (0)
Tìm x,y và z biết
1.\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)và x+y+z=18
2. \(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}\)và x-y+z=36
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{18}{9}=2\)
x/2=2=>4
y/3=2=>6
z/4=2=>8
\(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}=\frac{x-y+z}{5-6+7}=\frac{36}{6}=6\)
x/5=6=>30
y/6=6=>36
z/7=6=>42
Đúng 0
Bình luận (0)
\(\frac{x}{5}=\frac{y}{6}=\frac{z}{7}=\frac{x-y+z}{5-6+7}=\frac{36}{6}=6\) =>x=6.5=30;y=6.6=36;z=6.7=42
Đúng 0
Bình luận (0)
1. Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/2=y/3=z/4=x+y+z/2+3+4=18/9=2
Suy ra: x=2.2=4
y=3.2=6
z=4.2=8
Vậy x=4;y=6;z=8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x,y,z biết
n) \(\frac{x+1}{3}=\frac{y+2}{4}=\frac{Z+3}{5}vàx+y+z=18\)\(\)
O)\(\frac{x}{-3}=\frac{y}{-5}=\frac{Z}{-4}và3Z-2x=36\)
P) \(\frac{X}{4}=\frac{Y}{3}\)VÀ \(x.y=12\)
\(\text{Áp dụng dãy tỉ lệ bằng nhau ta được:}\)
\(\frac{x+1}{3}=\frac{y+2}{4}=\frac{z+3}{5}=\frac{x+y+z+6}{3+4+5}=\frac{24}{12}=2\)
\(\Rightarrow\hept{\begin{cases}x=2.3-1=5\\y=2.4-1=7\\z=2.5-3=7\end{cases}}\)
Đúng 0
Bình luận (0)
o) \(\frac{x}{-3}=\frac{y}{-5}=\frac{z}{-4}=\frac{2x}{2.\left(-3\right)}=\frac{y}{-5}=\frac{3z}{3.\left(-4\right)}=\frac{2x}{-6}=\frac{y}{-5}=\frac{3z}{-12}\)
Áp dụng tính chất DTSBN:
\(\frac{x}{-3}=\frac{y}{-5}=\frac{z}{-4}=\frac{2x}{-6}=\frac{y}{-5}=\frac{3z}{-12}=\frac{3z-2x}{-12-\left(-6\right)}=\frac{36}{-6}=-6\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=-6\Rightarrow x=-3.\left(-6\right)=18\\\frac{y}{-5}=-6\Rightarrow y=-5.\left(-6\right)=30\\\frac{z}{-4}=-6\Rightarrow z=-4.\left(-6\right)=24\end{cases}}\)
Vậy x = 18, y = 30, z = 24
p) \(\frac{x}{4}=\frac{y}{3}\Rightarrow\left(\frac{x}{4}\right)^2=\left(\frac{y}{3}\right)^2=\frac{xy}{4.3}=\frac{12}{12}=1\)
\(\Rightarrow\hept{\begin{cases}\left(\frac{x}{4}\right)^2=1\Rightarrow\frac{x^2}{16}=1\Rightarrow x^2=1.16=16=4^2\\\left(\frac{y}{3}\right)^2=1\Rightarrow\frac{y^2}{9}=1\Rightarrow y^2=1.9=9=3^2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x\in\text{{}4;-4\\y\in\text{{}3;-3\end{cases}}\)Nhớ thêm dấu ''}'' ở đằng sau -4 và -3 nhé
Vậy ...
Đúng 0
Bình luận (0)
n) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x+1}{3}=\frac{y+2}{4}=\frac{z+3}{5}=\frac{\left(x+y+z\right)+\left(1+2+3\right)}{3+4+5}=\frac{18+6}{12}=\frac{24}{12}=2\)
=>\(\frac{x+1}{3}=2=>x+1=2.3=6=>x=6-1=5\)
=>\(\frac{y+2}{4}=2=>y+2=4.2=8=>y=8-2=6\)
=>\(\frac{z+3}{5}=2=>z+3=2.5=10=>z=10-3=7\)
Vậy x=5;y=6;z=7
Đúng 0
Bình luận (0)
Vẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
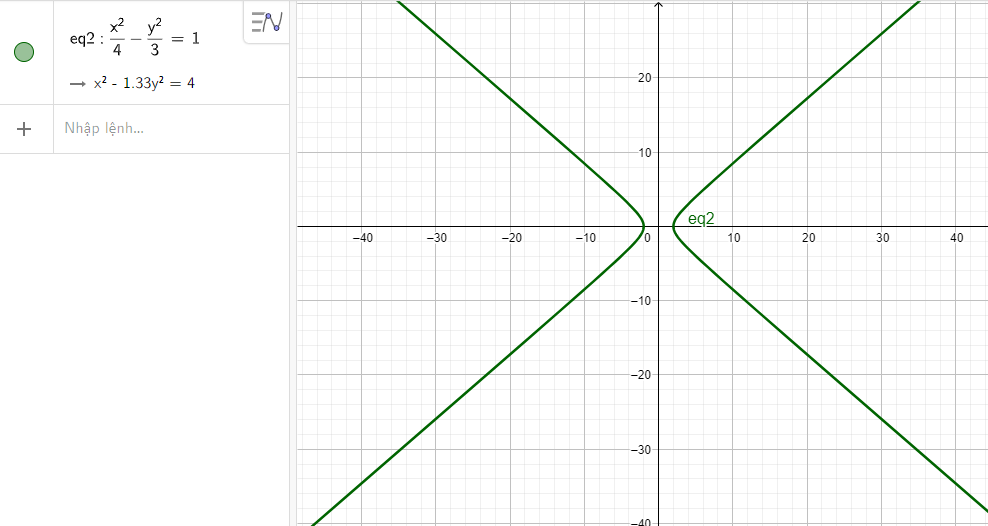
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Đúng 0
Bình luận (0)
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
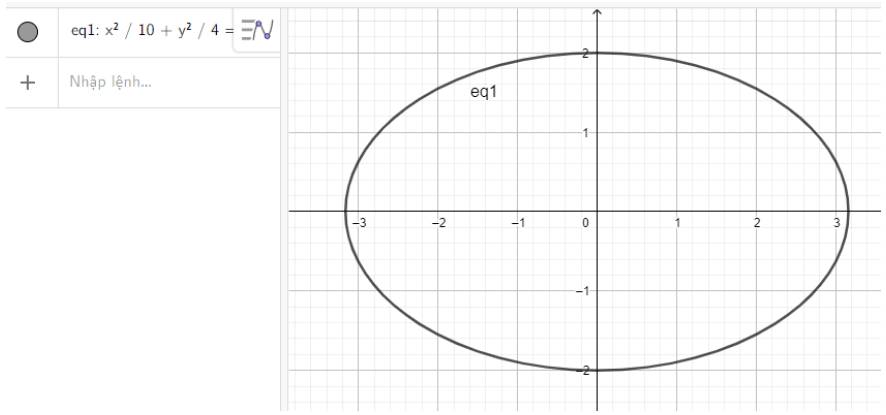
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
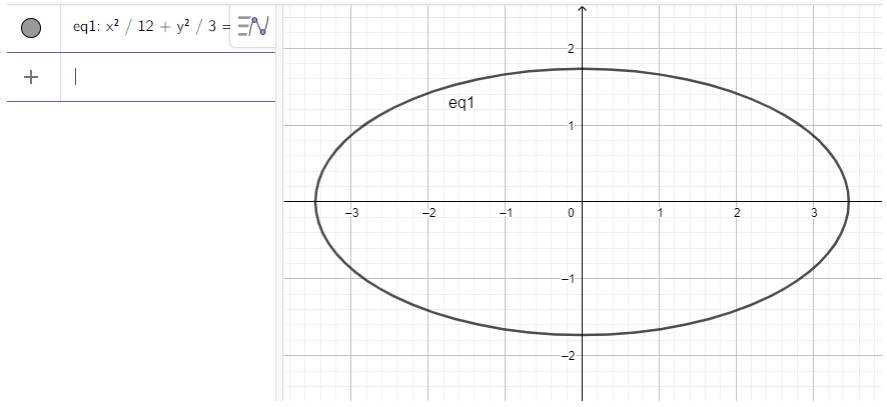
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
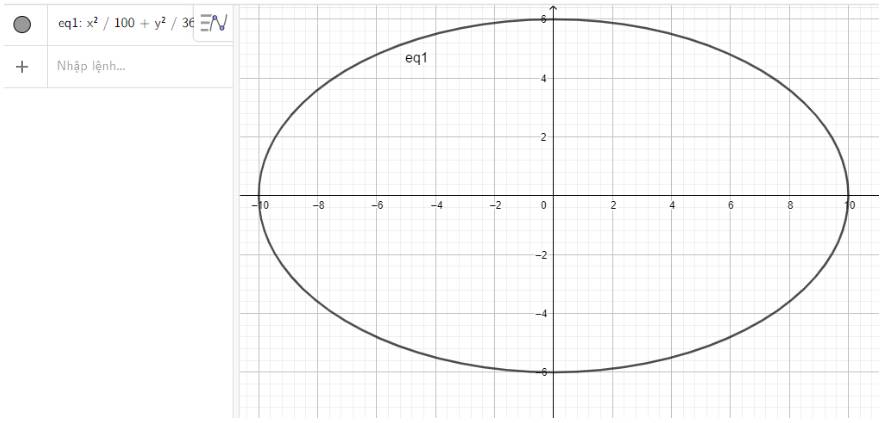
Đúng 0
Bình luận (0)
cho x,y,z khác 0 thỏa mãn: \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\). CMR: ( x+y+z). \(\left(\frac{1}{x}+\frac{4}{y}+\frac{9}{z}\right)\)= 36
Đặt: \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=k\)
\(\Rightarrow x=k\)
\(y=2k\)
\(z=3k\)
Thay x = k , y = 2k , z = 3k vào biểu thức cần cm ,ta đc:
\(\left(x+y+z\right)\left(\frac{1}{x}+\frac{4}{y}+\frac{9}{z}\right)=\left(k+2k+3k\right)\left(\frac{1}{k}+\frac{4}{2k}+\frac{9}{3k}\right)\)
\(=6k.\left(\frac{1}{k}+\frac{2}{k}+\frac{3}{k}\right)\)
\(=6k.\frac{6}{k}\)
\(=\frac{36k}{k}=36\)
=.= hok tốt!!
Đúng 0
Bình luận (0)
Đặt \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=k\)
Do đó \(x=k;y=2k;z=3k\)
Thay \(x=k;y=2k;z=3k\)vào \(\left(x+y+z\right).\left(\frac{1}{x}+\frac{4}{y}+\frac{9}{z}\right)\)ta có
\(\left(k+2k+3k\right).\left(\frac{1}{k}+\frac{4}{2k}+\frac{9}{3k}\right)\)
\(=6k.\left(\frac{6}{6k}+\frac{12}{6k}+\frac{18}{6k}\right)\)
\(=6k.\frac{6+12+18}{6k}\)
\(=\frac{6k.\left(6+12+18\right)}{6k}\)
\(=36\)
Do đó \(\left(x+y+z\right).\left(\frac{1}{x}+\frac{4}{y}+\frac{9}{z}\right)=36\)
Đúng 0
Bình luận (0)
Ta có:
\(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x+y+z}{1+2+3}=\frac{x+y+z}{6}\)(Tính chất dãy tỉ số bằng nhau
=> \(\hept{\begin{cases}\frac{x}{1}=\frac{x+y+z}{6}\\\frac{y}{2}=\frac{x+y+z}{6}\\\frac{z}{3}=\frac{x+y+z}{6}\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{x+y+z}{6}\\y=\frac{x+y+z}{3}\\z=\frac{x+y+z}{2}\end{cases}}\)
Đặt biểu thức cần chứng minh là A và x + y + z = k
=> \(\hept{\begin{cases}x=\frac{k}{6}\\y=\frac{k}{3}\\z=\frac{k}{2}\end{cases}}\)
=> A = \(k\left(\frac{1}{\frac{k}{6}}+\frac{4}{\frac{k}{3}}+\frac{9}{\frac{k}{2}}\right)\)
A = \(k.\left(\frac{6}{k}+\frac{12}{k}+\frac{18}{k}\right)=k.\frac{36}{k}=36\)(đpcm)
Đúng 0
Bình luận (0)
1) \(\frac{24}{-12}=\frac{x}{5}=\frac{-y}{3}\)Tìm x và y
2) \(\frac{1}{3}+\frac{-2}{5}+\frac{1}{6}+\frac{-5}{25}\le\frac{x}{10}< \frac{-3}{4}+\frac{4}{14}+\frac{-2}{8}+\frac{-3}{5}+\frac{5}{7}\)Tìm x
3) \(\frac{8.x+18}{2.x+6}\)Tìm x
1-(5\(\frac{5}{36}\)+y-7\(\frac{7}{18}\)):15\(\frac{3}{4}\)=0
\(1-\left(5\frac{5}{36}+y-7\frac{7}{18}\right):15\frac{3}{4}=0\)
=>\(1-\left(\frac{185}{36}+y-\frac{133}{18}\right):\frac{63}{4}=0\)
=>\(1-\left(-\frac{9}{4}+y\right).\frac{4}{63}=0\)
=>\(1-\left(-\frac{1}{7}+\frac{4}{63}y\right)=0\)
=>\(1+\frac{1}{7}-\frac{4}{63}y=0\)
=>\(\frac{8}{7}-\frac{4}{63}y=0\)
=>\(63.\frac{8}{7}-63.\frac{4}{63}y=63.0\)
=>\(72-4y=0\)
=>\(4y=72-0\)
=>\(4y=72\)
=>\(y=72:4\)
=>\(y=18\)
Đúng 0
Bình luận (4)
Xem thêm câu trả lời


