Chứng minh rằng:
Với a, b, c, d, e, thuộc N* và a/b < c/d thì a/b < (c+e)/ (d+e).
cho a,b,c,d,e,f thuộc N*
a/b>c/d>e/f và af-be=1. chứng minh rằng d>b+f
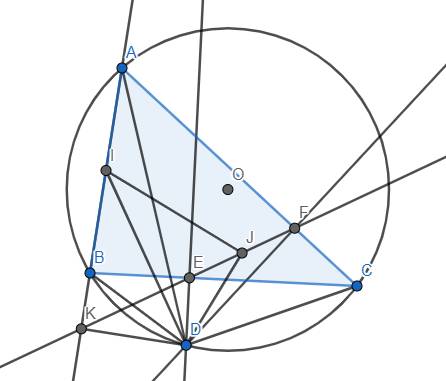
Cho tam giác $A B C$ có 3 góc nhọn nội tiếp dường tròn $(O)(A B<A C$ ). Gọi $D$ là điểm trên cung nhỏ $B C$ sao cho $D B<D C$. Từ $D$ kẻ $D E$ vuông góc với $B C$ (E thuộc $B C$ ), kẻ $D F$ vuông góc vổ $A C$ (F thuộc $A C$ ). Đường thẳng $E F$ cắt tia $A B$ tại $K$.
a) Chứng minh tứ giảc CDEF nội tiếp và $\widehat{ D F E}=\widehat{D A B} $.
b) Chứng minh tứ giác $D K B E$ nội tiếp và $D B \cdot D F=D A \cdot D E$.
c) Gọi I, J lần lượt là trung diểm của $A B, E F$. Chứng minh $I J$ vuông góc vởi $D J$.
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm
Chứng minh rằng \(a^b=b^c=c^d=d^e=e^a\)thì a = b = c = d = e
Câu hỏi của Nguyễn Ngọc Sơn Lâm - Toán lớp 7 - Học toán với OnlineMath
cho a,b,c,e,f thuộc Z+ biết a/b>c/d>e/f và af-be=1. Chứng minh d>b+f
Cho tam giác ABC( 5c A>90 d hat o ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh: a) A, D, B, E cùng thuộc một đường tròn. b) A,D,C,F cùng thuộc một đường tròn. c) B, C, E, F cùng thuộc một đường tròn .
Cho a,b,c,d,e \(\varepsilon N\) và \(a^b=b^c=c^d=d^e=e^a\) Chứng minh rằng ;a=b=c=d=e
Cho $\widehat{xOy}$. Lấy các điểm $A, \, B$ thuộc tia $O x$ sao cho $O A>O B$. Lấy các điểm $C, \, D$ thuộc $O y$ sao cho $O C=O A, \, O D=O B$. Gọi $E$ là giao điểm của $A D$ và $B C$. Chứng minh rằng
a) $A D=B C$.
b) $\triangle A B E=\triangle C D E$.
c) $O E$ là tia phân giác của $\widehat{x O y}$.
a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
Cho 5 số a,b,c,d,e\(\in n\)thỏa mãn:\(a^b=b^c=c^d=d^e=e^a\).Chứng minh rằng:a=b=c=d=e.
Giả sử a>b( trường hợp a<b chứng minh tương tự). Chú ý rằng nếu hai lũy thừa bằng nhau có cơ số( là số tự nhiên) khác nhauthì lũy thừa nào có cơ số nhỏ hơn sẽ có số mũ lớn hơn. Xong tiếp tục giải là ra
Bài1:Chứng minh rằng:
A=(7+72+73+...+78) chia hết cho 50
Bài2:Tìm x,y thuộc Z biết:
a) (x+5)(y-2)=-6
b)3x+4y-xy=15
Bài3:Cho a,b,c,d,e thuộc Z biết a+b+c+d+e=0 và a+b=c+d=d+e=2.Tính c,d,e
Bài 1 : Bài giải
Ta có :
\(A=7+7^2+7^3+...+7^8\)
\(A=\left(7+7^2+7^3+7^4\right)+\left(7^5+7^6+7^7+7^8\right)\)
\(A=7\left(1+7+7^2+7^3\right)+7^4\left(1+7+7^2+7^3\right)\)
\(A=7\cdot400+7^4\cdot400\)
\(A=7\cdot8\cdot50+7^4\cdot8\cdot50\)
\(A=50\left(7\cdot8+7^4\cdot8\right)\text{ }⋮\text{ }50\)
Bài 1 : Bài giải
Ta có :
\(A=7+7^2+7^3+...+7^8\)
\(A=\left(7+7^2+7^3+7^4\right)+\left(7^5+7^6+7^7+7^8\right)\)
\(A=7\left(1+7+7^2+7^3\right)+7^4\left(1+7+7^2+7^3\right)\)
\(A=7\cdot400+7^4\cdot400\)
\(A=7\cdot8\cdot50+7^4\cdot8\cdot50\)
\(A=50\left(7\cdot8+7^4\cdot8\right)\text{ }⋮\text{ }50\)
Bài 2 : Bài giải
a, \(\left(x+5\right)\left(y-2\right)=-6\)
\(\Rightarrow\text{ }\left(x+5\right)\text{ ; }\left(y-2\right)\inƯ\left(-6\right)\)
Ta có bảng :
| x + 5 | - 2 | - 3 | - 1 | - 6 |
| y - 2 | 3 | 2 | 6 | 1 |
| x | - 7 | - 8 | - 6 | - 11 |
| y | 5 | 4 | 8 | 3 |
Vậy \(\left(x\text{ ; }y\right)=\left(-7\text{ ; }5\right)\text{ ; }\left(-8\text{ ; }4\right)\text{ ; }\left(-6\text{ ; }8\right)\text{ ; }\left(-11\text{ ; }3\right)\)