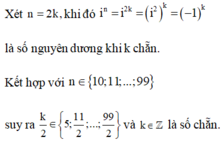Tập hợp các số nguyên dương n thỏa mãn 9<=3^n<82 là
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TP
Những câu hỏi liên quan
Tập hợp các số nguyên dương n thỏa mãn
81< 1/ 9* 27^ n < hoac =3^10
Tập hợp các số nguyên dương thỏa mãn 3n + 10 : n + 1
Ta có:\(\frac{3n+10}{n+1}=\frac{3n+3+7}{n+1}=\frac{3\left(n+1\right)+7}{n+1}=3+\frac{7}{n+1}\)
Để 3n + 10 : n + 1 là số nguyên dương khi 7 chia hết cho n+1
Hay \(n+1\inƯ\left(7\right)\)
Vậy Ư(7) là:[1,-1,7,-7]
Do đó ta có bảng sau:
| n+1 | -7 | -1 | 1 | 7 |
| n | -8 | -2 | 0 | 6 |
Đúng 0
Bình luận (0)
Ta có : 3n + 3+7 : ( chia hết) n+1
3n +3: n+1
=> 7 : n+1
n+1 = { 1 , 7 }
=> n=0 hoặc 6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tập hợp các số nguyên dương n thỏa mãn |2x+3| bé hơn hoặc bằng 5
ta có : l2x+3l < hoặc = 5
5 - 3 = 2
2x phải bằng 2 hoặc bé hơn 2
=>x thuộc {0;1}
thây x là 0 và 1
ta có : 2.0 + 3 = 3 < 5
2.1 + 3 = 5 = 5
suy ra : x thuộc 0;1
Đúng 0
Bình luận (0)
Tập hợp các số nguyên dương thỏa mãn 3n +10 chia hết cho n-1 là {...}
Ta có:
(3n + 10)⋮(n - 1)
⇒ [(3n - 3) + 13]⋮(n - 1)
⇒ [3(n - 1) + 13]⋮(n - 1)
Vì 3(n - 1)⋮(n - 1) nên để [3(n - 1) + 13]⋮(n - 1) thì 13⋮(n - 1)
⇒ n - 1 ∈ Ư(13)
⇒ n - 1 ∈ {1; -1; 13; -13}
⇒ n ∈ {2; 0; 14; -12}
Mà n là số nguyên dương
⇒ n ∈ {2; 14}
Vậy tập hợp A các số nguyên dương n thỏa mãn (3n + 10)⋮(n - 1) là:
A = {2; 14}
Đúng 0
Bình luận (0)
\(\frac{3n+10}{n-1}=\frac{3\left(n-1\right)+13}{n-1}=\frac{3\left(n-1\right)}{n-1}+\frac{13}{n-1}=3+\frac{13}{n-1}\in Z\)
\(\Rightarrow13⋮n-1\)
\(\Rightarrow n-1\inƯ\left(13\right)=\left\{1;-1;13;-13\right\}\)
\(\Rightarrow n\in\left\{2;0;14\right\}\) (n nguyên dương)
Đúng 0
Bình luận (0)
tập hợp các số nguyên dương n thỏa mãn 3n cộng 10 chia hết cho n-1
so do la:2;14
tk cho mk nhe
kb voi mk roi mk tk cho 3 lan luon
Đúng 0
Bình luận (0)
Giải :
Ta có : 3n + 10 chia hết cho n - 1 (1)
n - 1 chia hết cho n - 1
<=> 3 ( n - 1 ) chia hết cho n - 1
<=> 3n - 3 chia hết cho n - 1 (2)
Từ (1) và (2) => ( 3n + 10 ) - ( 3n - 3 ) chia hết cho n - 1
=> 13 chia hết cho n - 1 => n + 1 là ước của 13 là 1 ; 13
=> n = { 2 ; 14 }
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn i n là số nguyên dương. Số phần tử của S là
A. 22
B. 23
C. 45
D. 46
Đáp án A
Phương pháp giải:
Để i n là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n=2k khi đó ![]() là số nguyên dương khi k chẵn.
là số nguyên dương khi k chẵn.
Kết hợp với ![]() suy ra
suy ra 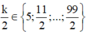 và
và ![]() là số chẵn.
là số chẵn.
Với mỗi bộ số 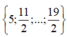 có 2 số k thỏa mãn,
có 2 số k thỏa mãn, 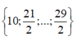 có 3 số k thỏa mãn.
có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4=22 số thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn i n là số nguyên dương. Số phần tử của S là
A. 22
B. 23
C. 45
D. 46
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn in là số nguyên dương. Số phần tử của S là
A. 22
B. 23
C. 45
D. 46
Đáp án A
Phương pháp giải:
Để in là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n = 2k, khi đó ![]() là số nguyên dương khi k chẵn
là số nguyên dương khi k chẵn
Kết hợp với ![]() suy ra
suy ra 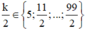 và k
∈
Z là số chẵn
và k
∈
Z là số chẵn
Với mỗi bộ số 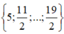 → có 2 số k thỏa mãn,
→ có 2 số k thỏa mãn, 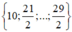 → có 3 số k thỏa mãn.
→ có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4 = 22 số thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Tìm số nguyên dương n thỏa mãn
1
+
P
1
+
2
P
3
+
3
P
3
+
.
.
.
+
n
P
n
P
2014
, với
P
n
là số các hoán vị của tập hợp có n phần tử. A. 2013 B. 2014 C. 2015 D. 2016
Đọc tiếp
Tìm số nguyên dương n thỏa mãn 1 + P 1 + 2 P 3 + 3 P 3 + . . . + n P n = P 2014 , với P n là số các hoán vị của tập hợp có n phần tử.
A. 2013
B. 2014
C. 2015
D. 2016
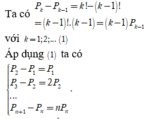
Cộng các đẳng thức ở (2) ta được ![]()
Do
P
1
=
1
![]()
Theo đề, ta có ![]()
Chọn A.
Đúng 0
Bình luận (0)