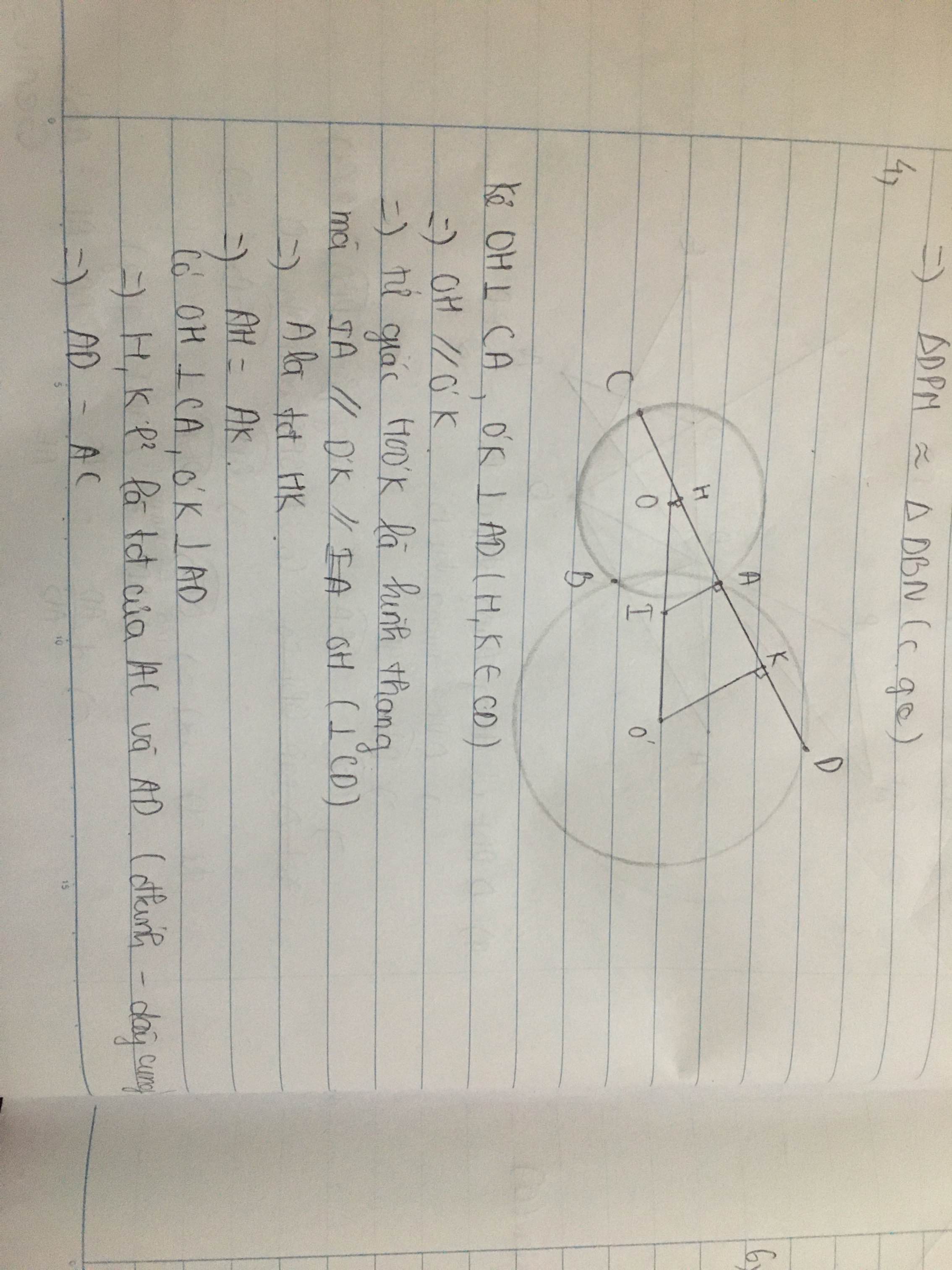Cho đường tròn (O) và (O’) cắt tại nhau A và B .Vẽ hình bình hành OCO’B . Chứng minh rằng AC//OO’
JJ
Những câu hỏi liên quan
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD
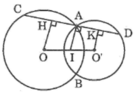
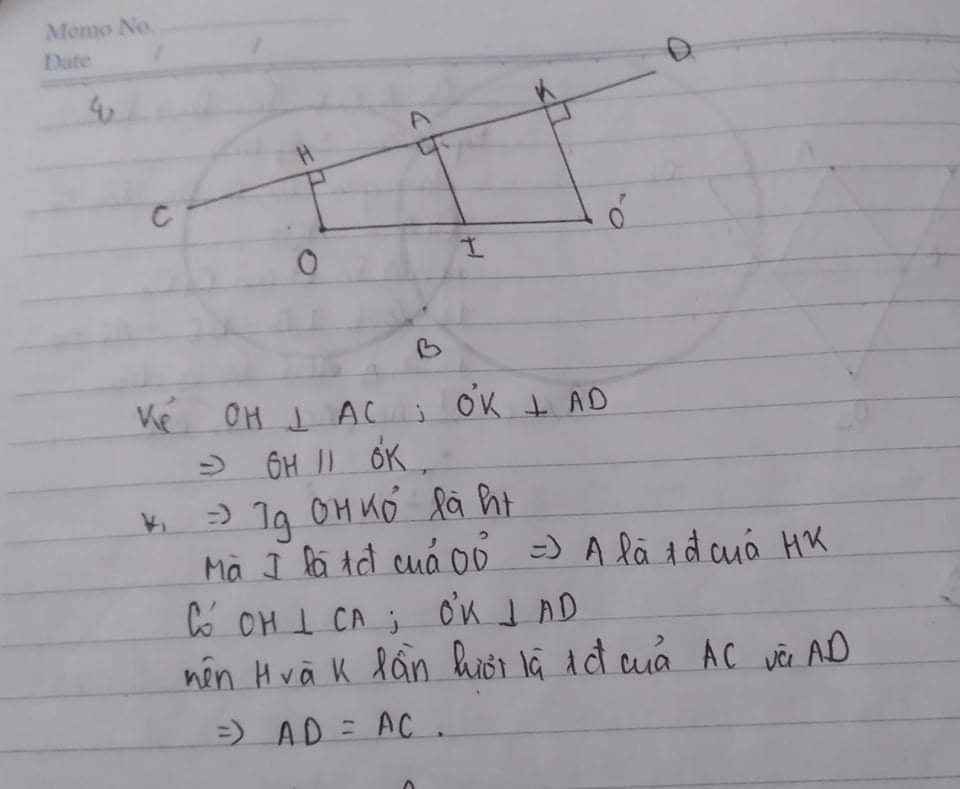
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Gọi I là trung điểm của OO'. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn )O) và (O') tại C vad D (khác A). Chứng minh rằng AC = AD ?
Cho hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A$ và $B$. Gọi $I$ là trung điểm của $OO'$. Qua $A$ vẽ đường thẳng vuông góc với $IA$, cắt các đường tròn $(O)$ và $(O')$ tại $C$ và $D$ (khác $A$). Chứng minh rằng $AC = AD$.
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
Cho 2 đường tròn (O,R) và (OR) cắt nhau tạo A và B ( O và O nằm khác phía với AB và góc OAO 90) Vẽ hình bình hành OAOEa) CM OEBO là hình bình hành (Cái này mình chứng minh đc r)b) Xác định tâm và bán kinh của đường tròn ngoại tiếp tam giác ABE ( câu này còn vế 2)c)Tiếp tuyến tại A của đường tròn (O) cắt (O) tại C(C khác A) tiếp tuyến tại A của đường tròn (O) cắt (O) tại D (D khác A) Gọi F là điểm đối xứng của A qua B. Chứng minh A,C,F,D cùng thuộc 1 đường tròn. d) Chứng minh S OAOB (OO^2+AB^2)/4
Đọc tiếp
Cho 2 đường tròn (O,R) và (OR') cắt nhau tạo A và B ( O và O' nằm khác phía với AB và góc OAO' >90) Vẽ hình bình hành OAO'E
a) CM OEBO' là hình bình hành (Cái này mình chứng minh đc r)
b) Xác định tâm và bán kinh của đường tròn ngoại tiếp tam giác ABE ( câu này còn vế 2)
c)Tiếp tuyến tại A của đường tròn (O') cắt (O) tại C(C khác A) tiếp tuyến tại A của đường tròn (O) cắt (O') tại D (D khác A) Gọi F là điểm đối xứng của A qua B. Chứng minh A,C,F,D cùng thuộc 1 đường tròn.
d) Chứng minh S OAO'B <=(OO'^2+AB^2)/4
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ cát tuyến chung MAN sao cho MA=AN. Đường vuông góc với MN tại A cắt OO' tại I. Chứng minh rằng I là trung điểm của OO'
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Trên AB lấy điểm E, trên CD lấy điểm F sao cho AE CF.a) Chứng minh: tam giác AEO tam giác CFOb) Chứng minh: E và F đối xứng nhau qua O.c) Từ E vẽ Ex // AC cắt BC tại I, vẽ Fy // AC cắt AD tại K.Chứng minh rằng: Tứ giác KEIF là hình bình hành.
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Trên AB lấy điểm E, trên CD lấy điểm F sao cho AE = CF.
a) Chứng minh: tam giác AEO = tam giác CFO
b) Chứng minh: E và F đối xứng nhau qua O.
c) Từ E vẽ Ex // AC cắt BC tại I, vẽ Fy // AC cắt AD tại K.
Chứng minh rằng: Tứ giác KEIF là hình bình hành.
Cho đường tròn tâm O đường kính AB. Lấy C thuộc đường tròn O sao cho AC>BC. Các tiếp tuyến tại A và C cắt nhau tại D. Vẽ hình bình hành BODE
a)Chứng minh B,C,E thẳng hàng
b)AE cắt OD tại F ; OE cắt CD tại H. Chứng minh HF song song AC
c)Chứng minh OC,DE,HF đồng quy