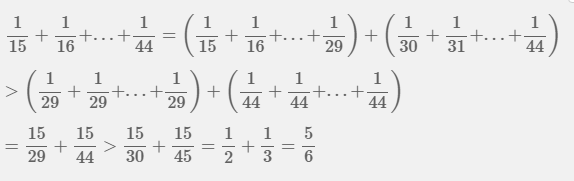Chứng minh rằng : 1/15 +1/16+1/17 +... +1/43+1/44 > 5/6
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
Chứng minh rằng
\(\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+...+\frac{1}{43}+\frac{1}{44}>\frac{5}{6}\)
Cho A = 1/15 + 1/16 + 1/17 +...+ 1/43 + 1/44
Chứng minh rằng A > 5/6
CÁC BẠN ƠI GIÚP MIK VỚI BÀI NÀY MIK SẮP PHẢI NỘP RÙI
Bài 3:
c) Chứng tỏ rằng \(\dfrac{1}{15}+\dfrac{1}{16}+\dfrac{1}{17}+...+\dfrac{1}{43}+\dfrac{1}{44}>\dfrac{5}{6}\)
Giúp mik vs! Thanks nhiều nha!
Câu1: CMR
1/15+1/16+1/17+....+1/43+1/44>5/6
Số lượng phân số của dãy số trên là:
(44-15):1+1=30 (phân số)
Ta chia dãy phân số thành 2 cặp. Mỗi cặp có 15 phân số
Ta có: 1/15+1/16+1/17+...+1/44>5/6
Lại có: 1/30<1/15;1/30<1/16;...;1/30<1/29
1/45<1/30;1/45<1/31;...;1/45<1/44
=> 1/30.15+1/45.15 < 1/15+1/16+1/17+...+1/44
=> 15.(1/30+1/45)< 1/15+1/16+1/17+...+1/44
=> 15.1/18< 1/15+1/16+1/17+...+1/44
=> 5/6 < 1/15+1/16+1/17+...+1/44 (đpcm)
Đúng 0
Bình luận (0)
Chứng minh rằng
\(\frac{1}{5}+\frac{1}{16}+\frac{1}{17}+...+\frac{1}{44}+\frac{1}{45}>\frac{5}{6}\)
Chung minh rang 1/15+1/16+1/17+1/18+.....+1/44 > 5/6
So sanh A va B:
\(A=\frac{1}{15}+\frac{1}{16}+\frac{1}{17}+...+\frac{1}{43}+\frac{1}{44}\)
\(B=\frac{5}{6}\)
1/15+1/16+1/17+..............+1/43+1/44>5/6
người nào làm đúng tích cho
Đặt A=1/15+1/16+1/17+1/18+.....+1/43+1/44
Dãy phân số có 30 phân số ta chia làm 2 nhóm mỗi nhóm 15 phấn số thì được:
A> 1/29+1/29+......1/29+1/44+1/44.....+1/44
A> 15 x 1/29 + 15 x 1/44
Suy ra: (dựa vào tính chất hai phân số có cùng tử số phân số nào có mẫu số lớn hơn thì phân số đó nhỏ hơn)
A> 15 x 1/30 +15 x 1/45
A>1/2 +1/3
A> 5/6
Đúng 0
Bình luận (0)
1. Chứng minh rằng : 1/5 +1/14 +1/28 +1/44 +1/61+ 1/85 +1/91 < 1/2
2. Chứng tỏ rằng : 1/5+1/6+1/7+...+1/16+1/17 < 2
3. Tính: A= [878787/9595953+ (-8787/9595)] * 1234621/5678765
4. So sánh : 10^8+2/10^8-1 ; B= 10^8/10^8-3
A=\(\frac{10^8+2}{10^8-1}=1+\frac{3}{10^8-1}\)
\(B=\frac{10^8}{10^8-3}=1+\frac{3}{10^8-3}\)
Vì\(10^8-1>10^8-3\)
\(\Rightarrow\frac{3}{10^8-1}< \frac{3}{10^8-3}\)
\(\Rightarrow1+\frac{3}{10^8-1}< 1+\frac{3}{10^8-3}\)
Vậy \(A< B\)
Đúng 0
Bình luận (0)