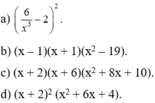Phân tích các đa thức sau thành nhân tử:(đặt biến phụ)
(x+1)(x+3)(x+5)(x+7)+15.
HELP ME!!!!!
RV
Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử:(đặt biến phụ)
(x+1)(x+3)(x+5)(x+7)+15.
Đặt \(A=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)
Ta có : \(A=\left[\left(x+1\right)\left(x+7\right)\right].\left[\left(x+3\right)\left(x+5\right)\right]+15=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
Đặt \(t=x^2+8x+11\) , suy ra \(A=\left(t-4\right)\left(t+4\right)+15=t^2-16+15=t^2-1=\left(t-1\right)\left(t+1\right)\)
\(\Rightarrow A=\left(x^2+8x+11-1\right)\left(x^2+8x+11+1\right)=\left(x^2+8x+12\right)\left(x^2+8x+10\right)\)
\(=\left(x+2\right)\left(x+6\right)\left(x^2+8x+10\right)\)
Đúng 0
Bình luận (0)
f(x) = (x+1)(x+3)(x+5)(x+7)+15
= (x+1)(x+7)(x+3)(x+5)+15
= (x2+7x+x+7)(x2+5x+3x+15)+15
= (x2+8x+7)(x2+8x+15)+15
Đặt X=x2+8x+11
f(x) = (X-4)(X+4)+15
= X2-16+15
= X2-12
= (X-1)(X+1)
=> f(x)= (x2+8x+11-1)(x2+8x+11+1)
f(x) = (x2+8x+10)(x2+8x+12)
Đến đây là vẫn còn phân tích được nhưng không dùng phương pháp đặt biến phụ:
f(x) = (x2+8x+10)(x2+8x+12)
= (x2+8x+10)[(x2+2x)+(6x+12)]
= (x2+8x+10)[x(x+2)+6(x+2)]
= (x+2)(x+6)(x2+8x+10)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử (x-1)(x-2)(x-3)(x-5)-15
cần gấp help me!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ta có (x-1)(x-2)(x-3)(x-4)-15=(x-1)(x-4)(x-2)(x-3)-15=\(\left(x^2-5x+4\right)\left(x^2-5x+6\right)-15\)(*)
đặt \(t=x^2-5x+5\)thì pt (*) =\(\left(t-1\right)\left(t+1\right)-15=t^2-1-15\)\(=t^2-16=\left(t+4\right)\left(t-4\right)=\)\(\left(x^2-5x+5+4\right)\left(x^2-5x+5-4\right)=\)\(\left(x^2-5x+9\right)\left(x^2-5x+1\right)\)
Đúng 0
Bình luận (0)
bạn cứ đọc kĩ đi cái đọan j ẩn phụ ý bạn thử thay t vào là hiểu
con đoạn nhân thì mình lấy cái cuối nhân cái đầu hai cái còn lại nhân vs nhau
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
phân tích đa thức thành nhân tử dạng đặt biến phụ
1, (x-1)(x-3)(x-5)(x-7)-20
2, (x-1)((x+2)(x+3)(x+6)-28
3, x(x-1)(x+1)(x+2)-3
1. (x-1)(x-3)(x-5)(x-7)-20=0
<=> (x-1)(x-7)(x-3)(x-5)-20=0
<=> (x^2-8x+7)(x^2-8x+15)-20=0
Đặt x^2-8x+7=a => x^2-8x+15= a+8
=> a(a+8)-20=0
<=> a^2+8a-20=0
<=>(a^2+8a+16)-36=0
<=> (a+4)^2=36
=> {a+4=6a+4=−6{a+4=6a+4=−6
<=>{a=2a=−10{a=2a=−10
*a=2 => x^2-8x+7=2
<=> x^2-8x+5=0
<=>(x^2-8x+16)-11=0
<=>(x-4)^2=11
<=>x-4=√11
<=> x=√11 +4
*a=-10 => x^2-8x+7=-10
<=> x^2-8x+17=0
<=> (x^2-8x+16)+1=0
<=> (x-4)^2=-1 (PT vô nghiệm)
Vậy pt có nghiệm x=√11 +4
mk chỉ biết vậy thôi
3, \(x\left(x-1\right)\left(x+1\right)\left(x+2\right)-3=\left(x^2+x\right)\left(x^2+x-2\right)-3\)
Đặt \(x^2+x=t\)
\(t\left(t-2\right)-3=t^2-2t-3=\left(t-3\right)\left(t+1\right)\)
Theo cách đặt \(\left(x^2+x-3\right)\left(x^2+x+1\right)\)
1, \(\left(x-1\right)\left(x-3\right)\left(x-5\right)\left(x-7\right)-20\)
\(=\left(x^2-8x+7\right)\left(x^2-8x+15\right)-20\)
Đặt \(x^2-8x+7=t\)
\(t\left(t+8\right)-20=t^2+8t-20=\left(t-2\right)\left(t+10\right)\)
Theo cách đặt \(\left(x^2-8x+5\right)\left(x^2-8x+17\right)\)
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ:a)
36
x
6
−
24
x
3
+
4
;
b)
(
x
2
-
1
)
2
- 18(x + l)(x -1);c) (x + l)(x + 3)(x + 5)(x + 7...
Đọc tiếp
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ:
a) 36 x 6 − 24 x 3 + 4 ;
b) ( x 2 - 1 ) 2 - 18(x + l)(x -1);
c) (x + l)(x + 3)(x + 5)(x + 7) +15;
d) ( x 2 + x + 4 ) 2 + 8x( x 2 + x + 4) + 15 x 2 .
phân tích đa thức thành nhân tử (thêm bớt cùng một hạng tử):
x^3 - 2x - 4
phân tích đa thức thành nhân tử (đặt biến phụ):
x^4 + 2x^3 + 5x^2 + 4x - 12
#)Giải :
\(x^3-2x-4\)
\(=x^3+2x^2-2x^2+2x-4x-4\)
\(=x^3+2x^2+2x-2x^2-4x-4\)
\(=x\left(x^2+2x+2\right)-2\left(x^2+2x+2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
\(x^4+2x^3+5x^2+4x-12\)
\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)
\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)
Đúng 1
Bình luận (0)
Câu 1.
Đoán được nghiệm là 2.Ta giải như sau:
\(x^3-2x-4\)
\(=x^3-2x^2+2x^2-4x+2x-4\)
\(=x^2\left(x-2\right)+2x\left(x-2\right)+2\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử ( đặt biến phụ):
a) (x^2+4x+8)^2+3x(x^2+4x+8)+2x^2
b) (x^2+x+1)(x^2+x+2)-12
c) (x^2+8x+7)(x^2+8x+15)+15
d) (x+2)(x+3)(x+4)(x+5)-24
đặt biến phụ Phân tích đa thức thành nhân tử
(x2 + x + 1)(x2 + x + 2) -12
(x2 + 8x + 7)(x2 + 8x + 15) + 15
(x + 2)(x + 3)(x + 4)(x + 5) -24
Giúp mình với mình đang gấp
Gợi ý:
a) Đặt \(t=x^2+x+1\)
b) Đặt \(t=x^2+8x+11\)
c) \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left[\left(x+2\right)\left(x+5\right)\right].\left[\left(x+3\right)\left(x+4\right)\right]-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt: \(t=x^2+7x+11\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử bằng cách đặt nhân biến phụ
(x+1)(x-4)(x+2)(x-8)+4x^2
(x+1)(x-4)(x+2)(x-8)+4x^2
=[(x+1)(x-8)][(x-4)(x+2)]+4x2
=(x2-7x-8)(x2-2x-8)+4x2
Đặt t=x2-2x-8 ta được:
(t-5x).t+4x2
=t2-5xt+4x2
=t2-xt-4xt+4x2
=t.(t-x)-4x.(t-x)
=(t-x)(t-4x)
thay t=x2-2x-8 ta được:
(x2-3x-8)(x2-6x-8)
Vậy (x+1)(x-4)(x+2)(x-8)+4x^2=(x2-3x-8)(x2-6x-8)
Đúng 0
Bình luận (0)
Dùng phương pháp đặt biến số phụ, phân tích các đa thức sau thành nhân tử
a. (x^2 + x)^2 - 2(x^2 + x) - 15
b. (x+2)(x+3)(x+4)(x+5) - 24
c. (x^2 + 8x + 7)(x^2 + 8x + 15) + 15
d. (x^2 + 3x + 1)(x^2 + 3x + 2) - 6
e. (4x+1)(12x-1)(3x+2)(x+1) - 4
f. 4(x+5)(x+6)(x+10)(x+12) - 3x^2
g. 3x^6 - 4x^5 + 2x^4 - 8x^3 + 2x^2 - 4x + 3