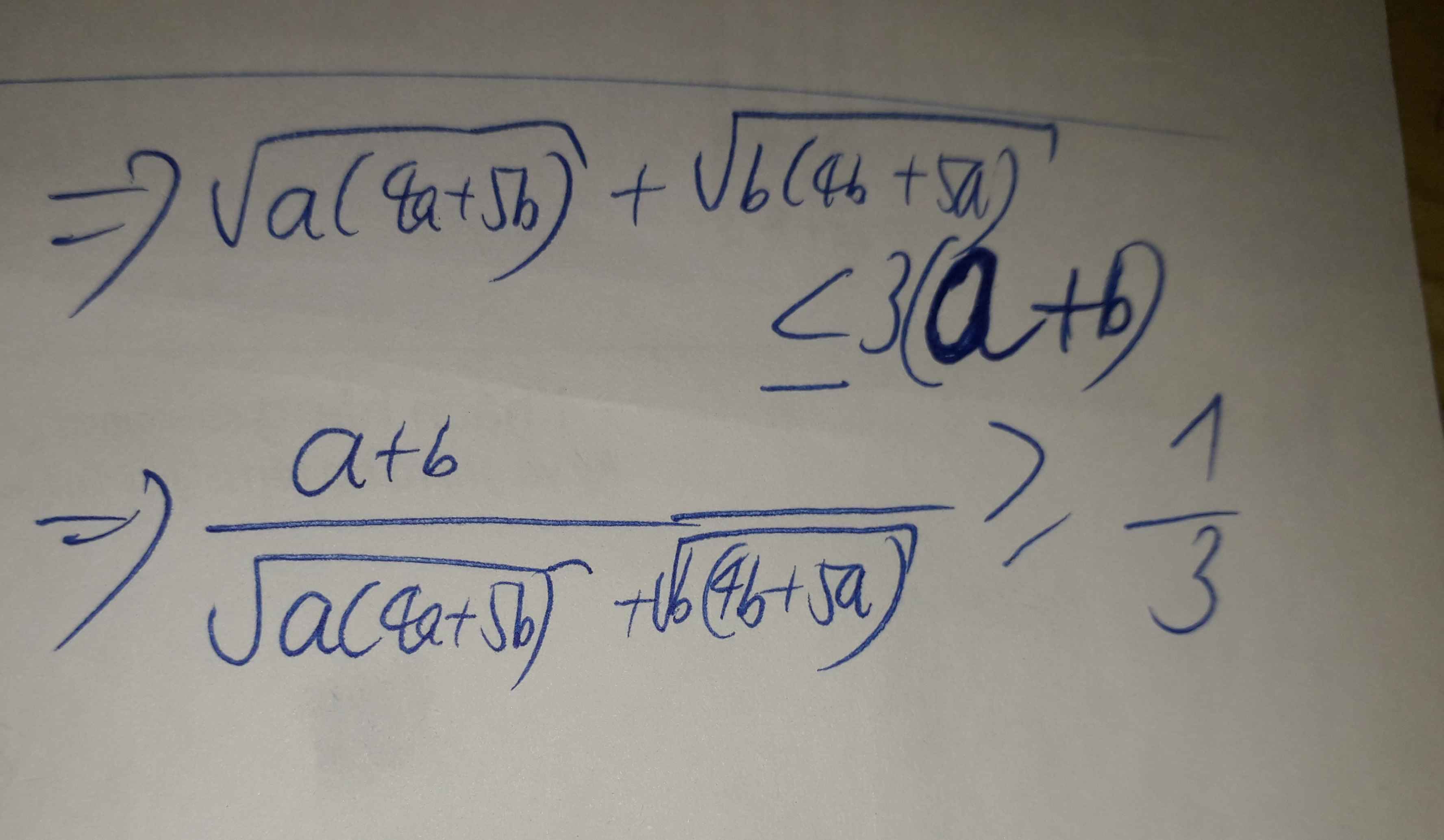cho biểu thức p=5a-b/4a+11 +5b-a/4b-11 với a#-11/4 và b#11/4. tính P khi a-b=11.
PL
Những câu hỏi liên quan
Cứu cứu
cho biểu thức p=5a-b/4a+11 +5b-a/4b-11 với a=-11/4 và b#11/4. tính P khi a-b=11.
Đính chính . Em viết sai điều kiện ạ.
Đúng phải là a#-11/4 và b#11/4
Cho biểu thức P = \(\dfrac{5a-b}{4a+11}\)+\(\dfrac{5b-a}{4b-11}\) với a\(\ne\)-\(\dfrac{11}{4}\) , b\(\ne\)\(\dfrac{11}{4}\)
Tính giá trị của P khi a - b = 11
\(a-b=11\)
\(P=\dfrac{5a-b}{4a+11}+\dfrac{5b-a}{4b-11}=\dfrac{5a-b}{4a+a-b}+\dfrac{5b-a}{4b-\left(a-b\right)}\)
\(=\dfrac{5a-b}{5a-b}+\dfrac{5b-a}{5b-a}\)
\(=2\)
Vậy...
Đúng 5
Bình luận (0)
Tính giá trị của biểu thức:
A=7a + 7b với a+b= 11
B= 13a + 19b + 4a - 2b với a+b=100
C=5a - 4b + 7a - 8b với a-b =8
a) \(A=7a+7b=7\left(a+b\right)=7.11=77\)
b) \(B=13a+19b+4a-2b=17a+17b=17\left(a+b\right)=17.100=1700\)
c) \(C=5a-4b+7a-8b=12a-12b=12\left(a-b\right)=12.8=96\)
Đúng 0
Bình luận (0)
Cho hai số a, b dương. Tìm giá trị nhỏ nhất của biểu thức:
\(P=\dfrac{a+b}{\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}}\)
cho a,b là 2 số nguyên dương .Tìm GTNN của biểu thức sau
\(P=\frac{a+b}{\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}}\)
\(P=\frac{3\left(a+b\right)}{\sqrt{9a\left(4a+5b\right)}+\sqrt{9b\left(4b+5a\right)}}\)
\(\ge\frac{3\left(a+b\right)}{\frac{9a+4a+5b}{2}+\frac{9b+4b+5a}{2}}=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Ta có :
\(P^1=\frac{a+b}{\sqrt{a\left(4a+5b\right)}+\sqrt{b\left(4b+5a\right)}}.\)
\(\Leftrightarrow P^2=\frac{3\left(a+b\right)}{\sqrt{9a\left(4a+5b\right)}+\sqrt{9b\left(4b+5a\right)}}\)
Mà ta thấy biểu thức \(P^2\ge\frac{3\left(a+b\right)}{\frac{9a+4a+5b}{2}+\frac{9b+4b+5a}{2}}\)
\(=\frac{1}{3}\)
Vậy giá trị nhỏ nhất của biểu thức \(P=\frac{1}{3}\)
\(\)
Đúng 0
Bình luận (0)
(4a+5b+7c) chia het cho 11. Cmr (5a+9b+6c) chia het cho 11 với a,b,c là số tự nhiên
cho tỷ lệ thức a/b=c/d. chứng minh:
a, 2a+5b/3a-4b=2c+5d/3c-4d
b. 3a+7b/5a-7b=3c+7d/5c-7d
d. 4a+9b/4a-7b=4c+9d/4c-7d
giúp mình với ạ
Ho a,b,c E N.bieets (4a+5b+7c) chia het cho 11,cmr (5a+9b+6c) chia hết cho 11
hi!hi! 2 cái l ike là tớ tròn 1600 điểm hỏi đáp
Đúng 0
Bình luận (0)
Cho a,b,c thuộc N. Biết (4a+5b+7c) chia hết cho 11. CMR (5a+9b+6b) cjia hết cho 11