Ta có  D H ⊥ A B ;   C K ⊥ A B nên DH//CK.

Vì ABCD là hình bình hành nên AB//CD hay HK//CD.

Xét tứ giác HKCD có : DH // CK và HK // CD nên tứ giác HKCD là hình bình hành.

Xét tam giác DHA và tam giác CKB là hai tam giác vuông có :

DH=CK (vì HKCD là hình bình hành)

AD=BC (vì ABCD là hình bình hành)

Suy ra  DHA= CKB (ch.cgv)

Suy ra HA = KB (2 cạnh tương ứng)

Chọn đáp án B.

* Ta có: 

nên DH // CK.

Vì ABCD là hình bình hành nên AB // CD hay HK// CD.

Xét tứ giác HKCD có: DH// CK và HK// CD nên tứ giác HKCD là hình bình hành.

* Xét ΔDHA và ΔCKB có:

DH = CK (vì HKCD là hình bình hành)

AD = BC (vì ABCD là hình bình hành)

Suy ra: ΔDHA = ΔCKB (c.g.c)

Suy ra: HA = KB ( 2 cạnh tương ứng)

Chọn đáp án B

Lời giải:
a. 

Ta có: $ab=BCNN(a,b).ƯCLN(a,b)$

$\Rightarrow 1200=3.ƯCLN(a,b).ƯCLN(a,b)$

$\Rightarrow ƯCLN(a,b).ƯCLN(a,b)=400=20.20$
$\Rightarrow ƯCLN(a,b)=20$ 

Đặt $a=20x, b=20y$ với $x,y$ là 2 số nguyên tố cùng nhau.

Khi đđ:

$ab=20x.20y$

$\Rightarrow 1200=400xy\Rightarrow xy=3$

Kết hợp với $x,y$ nguyên tố cùng nhau $\Rightarrow (x,y)=(1,3), (3,1)$ 

$\Rightarrow (a,b)=(20, 60), (60,20)$

b. Đề không rõ ràng. Bạn viết lại nhé.

s

s

Chọn B.

có ai lm đc ko

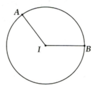
a,  A I B ^ = 120 0  là góc tâm của (O; R) nên sđ  A B ⏜ = 120 0

Áp dụng công thức tính độ dài cung tròn  l = πRn 180  với R = 2cm;  n 0 = 120 0

Độ dài cung nhỏ AB là:  l = π . 2 . 120 180 = 4 π 3 cm

b, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB là phần tô màu xám

Áp dụng công thức:  S = πR 2 n 360  với R = 2cm;  n 0 = 120 0

Tính được S =  4 π 3 c m 2

Đáp án là B 

Đáp án B

V = 1 3 . S A . S A B C = 1 3 . S A . 1 2 . A B . A C . sin B A C = 1 3 . a . 1 2 . a . 2 a . sin 120 0 = a 3 3 6