trong mặt phẳng tọa độ tìn vị trí các điểm có tọa độ x;y thảo mãn 1 trong các điều kiện
a) Điểm A : x(y-1)=0
b ) Điểm B : (x+y)(y-2)=0
c ) Điểm C : (x-1)^2+(y+2)^2=0
PH
Những câu hỏi liên quan
trong mặt phẳng tọa độ Oxy, tìm vị trí các điểm có tọa độ ( x,y ) thỏa mãn x²+y²-2x+4y = 0
Xem chi tiết
ta có
\(x^2+y^2-2x+4y=0\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=5\)
Vậy tập hợp các điểm thỏa mãn phương trình trên là đường tròn tâm I( 1,-2) bán kính \(\sqrt{5}\)
trong mặt phẳng tọa độ oxy, tìm vị trí các điểm có tọa độ x,y thỏa mãn : (x-1)^2 + (y+2)^2=0
Trên mặt phẳng tọa độ có đường tròn tâm M, bán kính 3 cm. Tọa độ điểm M là (3; -2). Đường tròn tâm M có vị trí như thế nào đối với các trục tọa độ
Đọc tiếp
Trên mặt phẳng tọa độ có đường tròn tâm M, bán kính 3 cm. Tọa độ điểm M là (3; -2). Đường tròn tâm M có vị trí như thế nào đối với các trục tọa độ
Trên mặt phẳng tọa độ cho điểm I có tọa độ (-3; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí như thế nào đối với các trục tọa độ?
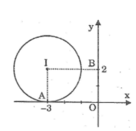
Kẻ IA ⊥ Ox
Ta có: IA = 2 = R
Suy ra đường tròn (I) tiếp xúc với trục hoành
Kẻ IB ⊥ Oy
Ta có : IB = 3 > R
Suy ra đường tròn và trục tung không có điểm chung
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, vẽ đường tròn (A,2cm). biết tọa độ của điểm A(-3,2)
a, Đường tròn tâm A có vị trí như thế nào đối với trục tọa độ.
b, Điểm O (gốc tọa độ) có vị trí như thế nào đối với đường tròn tâm A
Trên mặt phẳng tọa độ có đường tròn tâm M bán kính 3cm.Tọa đọ điểm M là (3;-2).Đường tròn tâm M có vị trí ntn với các trục tọa độ
Trên mặt phẳng tọa độ Oxy, cho điểm A( 5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?
A. Đường tròn tiếp xúc trục Oy.
B. Đường tròn tiếp xúc với trục Ox.
C. Đường tròn không cắt trục Ox.
D. Đường tròn không cắt trục Oy.
Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, cho điểm B(2; 4). Hãy xác định vị trí tương đối của đường tròn (B; 3) và các trục tọa độ
(B) Cắt Oy tại hai điểm phân biệt và (B) không cắt Ox
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ
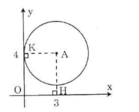
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
Đúng 0
Bình luận (0)